如何理解单自由度系统振动

一、数学模型
二、自由振动
    2.1无阻尼自由度振动
    2.2有阻尼自由度振动
三、受迫振动
    3.1 无阻尼受迫振动（正弦激励）
    3.2 有阻尼受迫振动（正弦激励）
    3.3 有阻尼受迫振动（阶跃激励）
    3.4 有阻尼受迫振动（冲击响应）

一、数学模型

对于很多工程而言，动态特性是非常重要的考核指标，其本质就是两个变量及其关系： 力 和 位移 。对于对象可以简化成质点或者刚体的问题，这个问题其实伟大的牛爵士已经解决了，即牛顿第二定律：

对应的力我们称之为惯性力，实际工程上和位移相关的不仅仅有 惯性力 ，还有其它的力，比如和速度相关的（位移的导数） 阻尼力 ，以及和位移线性相关的 弹性力 ，同时包含惯性力、阻尼力和弹性力的模型就是我们常说的 单自由度弹簧振子 系统，具体数学模型如下：

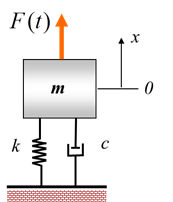
则根据力平衡方程，可以得到：

其中： ——质量块质量； ——阻尼系数； ——弹簧刚度； ——质量块位移； ——外界施加力。

对上式两端进行拉普拉斯变换，可以的到：

即系统的传递函数为：

从数学上看，这是一个典型的二阶系统，我们知道，绝大多数工程中系统都可以降阶为一阶系统和二阶系统的叠加，一阶系统非常简单，通过我们关注的和难解决的都是二阶分量对应的模态，因此理解如上单自由度弹簧振子模型（二阶系统）的响应特性非常重要。

从物理上看，对于单自由度系统而言，都可以简化为如上模型；当系统是更复杂的连续系统时，一般更关心一阶模态的振动（动态特性），这也可简化成单自由度振动，因此理解单自由度系统振动是理解其他一切振动的基础。

比如，对于飞机的飞行控制，其实就是将飞机的纵向运动降阶为两个二阶运动（长周期运动和短周期运动），进而加以控制，具体见下文：

https:// zhuanlan.zhihu.com/p/91 047110

单自由度系统的振动可以分成两大部分： 自由振动（无外力 ） 和 受迫振动（有外力 ） 。

二、自由振动

当 时，称弹簧振子系统为自由振动，根据系统中阻尼的情况，自由振动又可分为 无阻尼 自由振动和 有阻尼 自由振动。为简单起见，先分析无阻尼自由振动。

2.1无阻尼自由振动

当系统为 无阻尼自由 振动时，对弹簧振子而言，其机械能是守恒的，振动的本质就是动能和势能之间的互相转换，系统做等幅振动。

此时，阻尼系数 ，带入振动方程有：

设

则振动方程可以改写为：

这是一个典型的二阶微分方程，其通解形式为：

或者写成更紧凑的形式：

设系统的初始条件为： 时，有 ， ，则带入微分方程的通解可以得到：

即方程的解为：

当通解写成指数形式时，可以得到：

二阶线性振动微分方程的解释时间 的简谐函数，方程解中的 只决定于系统本身的参数 和 ，而与系统的初始条件无关，是系统本身的固有特性，称之为 固有频率 。方程解中的 称为振幅，是质量块偏离静平衡位置的最大距离， 称为初相位。

搭建仿真模型如下：

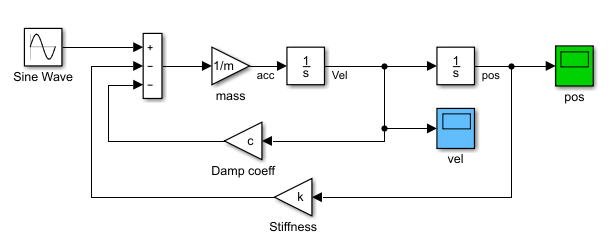
xi=0;%阻尼比为0
wn=1;%固有频率为1rad/s； 

m=1;%质量为1Kg；
k=m*wn^2;%刚度，N/m；
c=2*sqrt(m*k)*xi; %阻尼系数，N/(m/s)
F0=0; %正弦激励振幅，m；
w=0.5;%正弦激励频率，rad/s； 

v0=1; %初始速度，m/s；
x0=2; %初始位移，m；

仿真波形如下：

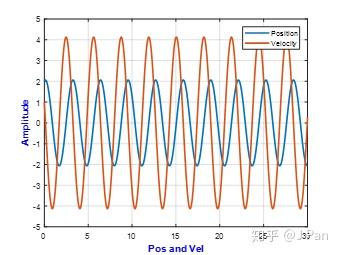
可见，对于无阻尼自由振动，当有初始速度/位移时，系统做 等幅振动 。

2.2有阻尼自由振动

无阻尼系统振动过程中能量守恒，振幅保持不变。而实际情况并非如此，必须考虑阻力对振动过程的影响。

实际阻力的形式很多，有滑动表面的阻力、空气等流体阻力、弹性材料的内摩擦阻力等，因此阻力的大小变化规律等也各不相同。

当系统为 有阻尼自由 振动时，对弹簧振子而言，就是机械能不断转化为热能的过程，振动的本质就是动能和势能之间的互相转换，并最终都转换为热能，因此振动的幅值是逐渐减小的。

此时振动方程为：

假设阻尼比为：

则振动方程可改写为：

令其解为：

带入到振动方程，可以得到：

此特征方程的两个根是：

不同的阻尼比，对应的解的形式不同，运动性质也不同。

a） （过阻尼）

此时特征方程有两个不同的实根，通解为：

给出初始条件： 时， 则可以确定系数和分别为：

这种情况对应的运动时一种衰减运动，但不是我们关心的振动形式。设 ，则运动图形大致如下：

%%
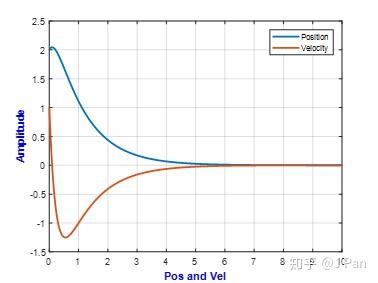
xi=1.3;wn=2;
m=1;k=m*wn^2;c=2*sqrt(m*k)*xi;F0=0;w=0.5;
v0=1;x0=2;

b） （临界阻尼）

此时特征方程有重根，通解为：

利用初始条件确定常数为：

此时的阻尼系数成为临界阻尼系数，记为，数值为：

临界阻尼情况也是一种非振动形式的衰减运动，按不同的初始条件，其运动图形如下：

%%
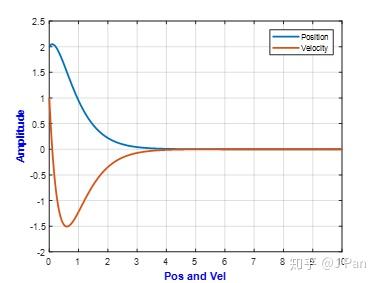
xi=1.0;wn=2;
m=1;k=m*wn^2;c=2*sqrt(m*k)*xi;F0=0;w=0.5;
v0=1;x0=2;

c） （欠阻尼）

此时特征方程有一对共轭复根，通解为：

或者写成跟紧凑的指数形式：

利用初始条件，确定出常数为：

指数形式的常数为：

解中有两个因子，一个是衰减的指数函数 ，它将使振幅越来越小，直至振动最终消失；另一个因子是正弦函数 ，它表示系统以相同的周期通过平衡位置。因此，系统总的呈现形式为一种衰减的等周期振动。

%%
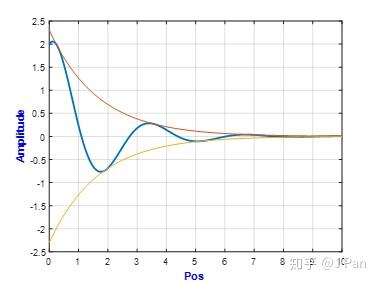
xi=0.3;wn=2;
m=1;k=m*wn^2;c=2*sqrt(m*k)*xi;F0=0;w=0.5;
v0=1;x0=2;

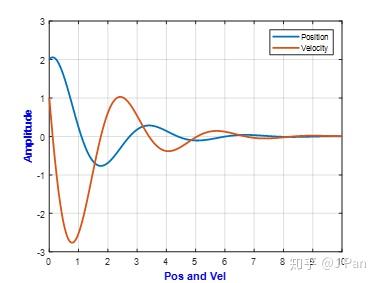
振幅衰减的快慢可以用相邻振幅的比值来表示，称之为衰减率，也可以用衰减率的自然对数来表示，称之为对数衰减率。

根据前面给出的解：

令：

称之为 有阻尼固有频率 ，其对应的周期为：

这样可以得到相邻周期幅值的 衰减率 为：

对数衰减率为：

同理，任意两个相邻的周期之间幅值的衰减率是固定的，有：

则有：

所以有：

可以得到：

即：

这样就可以根据幅值衰减率反算出系统的阻尼器比。

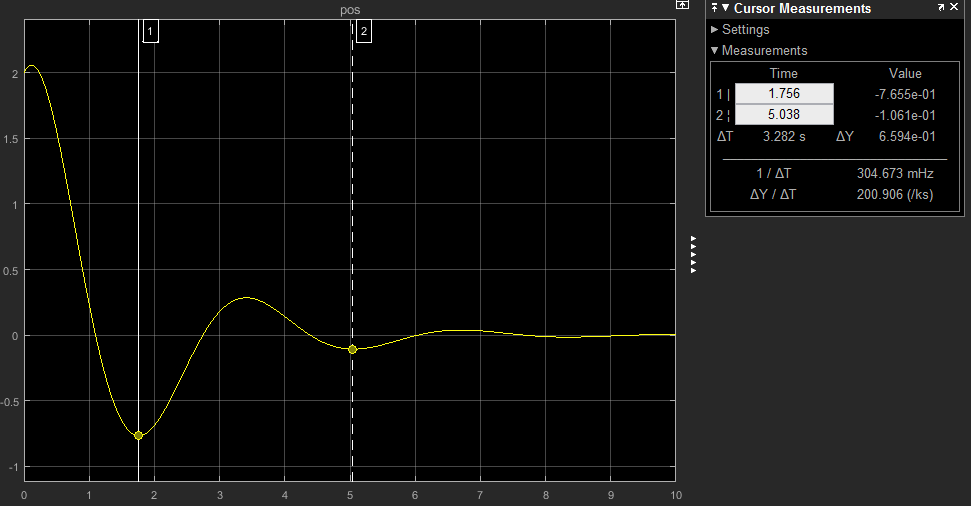
比如在上图中，相邻两个波谷处的幅值衰减率为 ，对应的对数衰减率为： ，可以就可以反算出系统的阻尼比为：

与之前的仿真时设置的阻尼比是完全一致的。

三、受迫振动

系统在外部激励下的振动称之为受迫振动或者强迫振动。自由振动只是系统对初始扰动（初始条件）的响应。由于阻尼的存在，振动现象很快消失，要使振动持续进行，必须有外界的激励输入给系统以补充阻尼消耗的能量。

3.1 无阻尼受迫振动（正弦激励）

无阻尼受迫振动的本质是系统内部的机械能（动能、势能之和）和外界做功的能量互相转换，同时系统内部的动能和势能之间也互相转换，可见整个过程是比较复杂的。

此时振动微分方程为：

无阻尼受迫振动的通解的形式前面已经给出，

假设其特解为：

则有：

给出初始条件： 时 ，则可以确定系数和分别为：

同时可以得到：

假设：

则有：

所以可以得到无阻尼受迫振动的解为：

可见，对于无阻尼受迫振动，振动的解分为三个部分：

1. 与初始条件有关的 初始条件响应 ，和初始条件相关，以固有频率振动；
2. 系统受到扰动后的 自由伴随振动 ，与初始条件无关，也是以固有频率振动；
3. 强迫响应 ，振动频率为外界激励频率。

曲线响应如下：

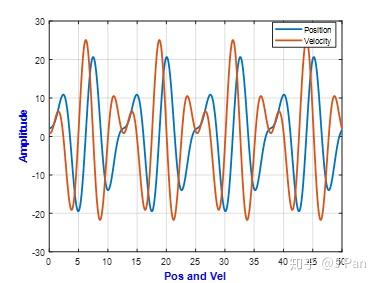
该曲线为两个正弦曲线的叠加，一个为固有频率1rad/s，一个为受迫频率1.5rad/s，具体参数如下表所示。

%%
xi=0;wn=1;
m=1;k=m*wn^2;c=2*sqrt(m*k)*xi;F0=10;w=1.5;
v0=1;x0=2;

若激励频率与固有频率十分接近，即：

则会出现所谓的 “拍振” 现象。不妨假设：

其中 为一个小量。

假设系统为零初始条件，即 ，则系统的解可以简化为：

将 带入可以得到：

忽略 小量，得到：

根据三角函数和差化积，可以得到：

当 比较小时，有 ，所以有：

同上， ，所以有：

可见，对于无阻尼受迫振动而言，当外界激励频率与系统固有频率接近时，系统响应可以看成是振动频率为 ，振幅按 规律变换的振动，如下图所示：

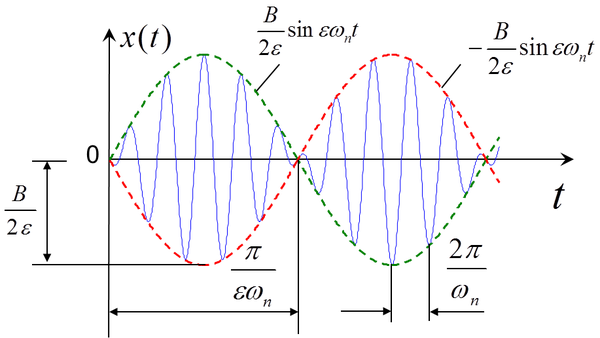
这种在接近共振时发生的特殊的振动现象称为“拍”，这种振动称为“ 拍振 ”，“拍”的周期为 ，图形的包络线为 。

%%
xi=0;wn=2;
 
m=1;k=m*wn^2;c=2*sqrt(m*k)*xi;F0=1;w=1.8;
 
v0=1;x0=2;

系统响应曲线如下：

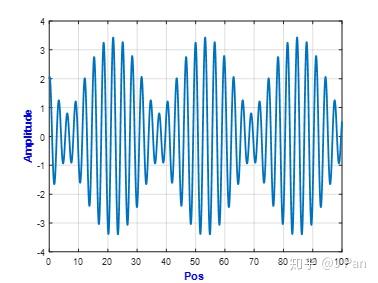
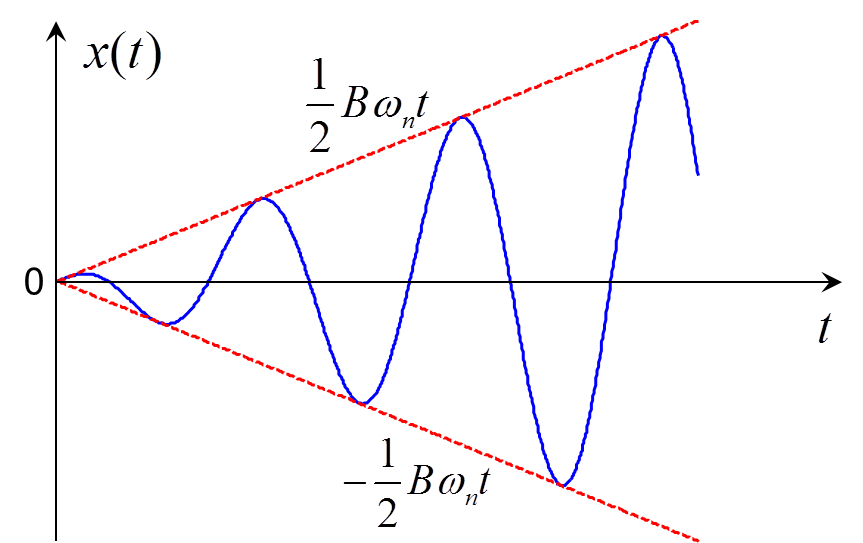
当 时，有：

3.2 有阻尼受迫振动（正弦激励）

有阻尼的受迫振动是最为复杂的单自由度振动，有阻尼受迫振动的本质是系统内部的机械能（动能、势能之和）和外界做功的能量互相转换，同时系统内部的动能和势能之间以及和热能之间也互相转换。

有阻尼受迫振动的响应分两部分， 稳态响应 和 瞬态响应 。

我们先分析 稳态响应 （幅值响应和相位响应），再分析 瞬态响应 。先看稳态响应：

完整的微分方程如下：

假设其 稳态解 为：

带入方程，可以得到系数幅值响应 和相位响应 分别为：

其中：

可见：

1）在简谐激励条件下，响应也是简谐的，响应频率与激振频率相同；

2）简谐激励强迫振动的振幅 和相位角 决定于系统本身的物理特性和激振力的大小于频率，与初始条件无关。

对于稳态响应，定义放大系数 为响应的振幅 与激振力 所引起的静位移比值：

以 为参数，画出 曲线，即幅频特性曲线，表明了阻尼和激振频率对响应幅值的影响。

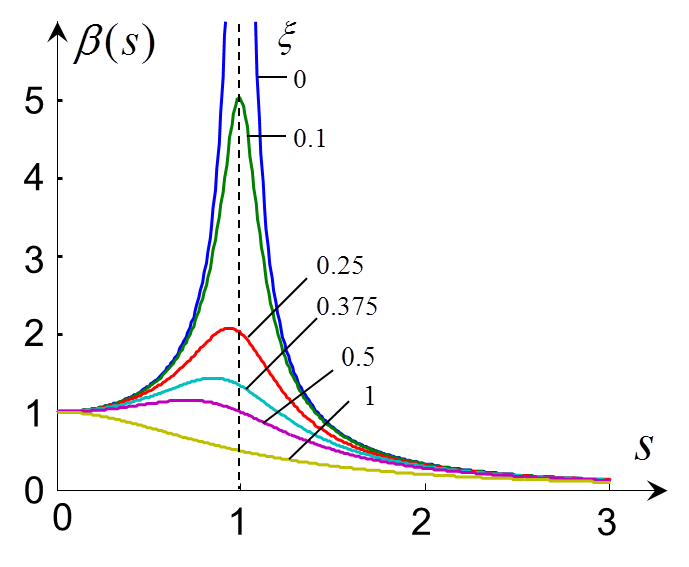
讨论：

1） 时，放大系数为：

即响应幅值近似等于激振力幅值所引起的静位移。

2） 时，放大系数为：

即响应幅值近似等于0，高频下系统来不及响应。

3） 时，

激振频率接近固有频率， 迅速增大，振幅很大，这种现象称为共振。阻尼比越小，共振越厉害，因此了解系统的共振频率非常重要。

为求取共振频率，先对频率比微分：

令 ，可以得到：

所以有：

可以得到放大倍数为：

可见对于有阻尼受迫振动而言，系统的响应不会是无穷大，是有限值 ，而响应最大的频率为 ，既不是无阻尼固有频率，也不是阻尼固有频率，这个我们一般的认识是有偏差的（激励频率为固有频率时响应最大）。也就是说，只有在阻尼比为零时，我们所说激励频率为固有频率时（无论是无阻尼固有频率还是有阻尼固有频率），系统共振（响应最大）才成立，此时， 。

实际工程上，系统自身的阻尼比一般都不太大，此时在固有频率处（ ）的放大倍数为：

可见，当阻尼比 很小时， 和 相差很小，所以在工程中仍认为 时发生共振。

前面介绍了幅值响应，现在看一下相位响应。

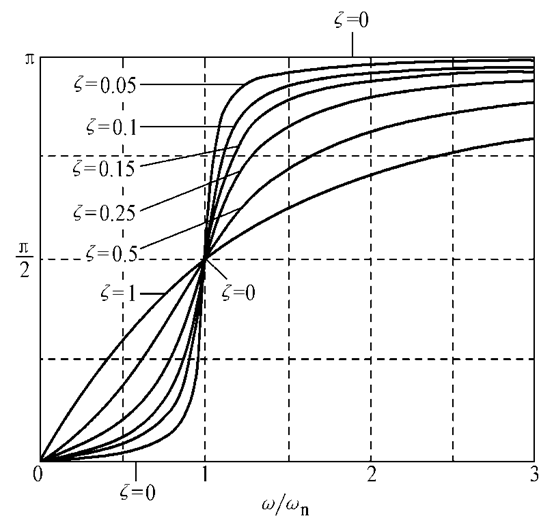
讨论：

1） 时，相位差为：

位移与激振力在相位上几乎相同。

2） 时，相位差为：

位移与激振力反相；

3） 时，

共振时的相位差为 ，与阻尼无关。

对于 ，随着 的变化，相位响应在 处有突变，从 调到 时的 。

前面介绍了 稳态响应 ，现在看一下 瞬态响应 。完整的振动方程为：

方程的完整解为瞬态部分和稳态部分的叠加，即：

初始条件为： 时 ，带入振动方程可以得到：

所以线性有阻尼振动在正弦激励作用下的响应最终表示为：

其中

分别为稳态响应的幅值响应和相位响应。系统的全响应 和强迫响应 示意图如下：

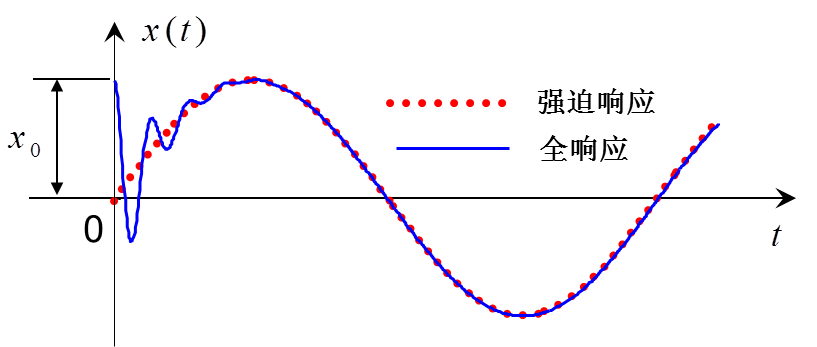
3.3 有阻尼受迫振动（阶跃激励）

如果输入为单位阶跃信号，则振动方程为：

由于实际工程中系统一般均为欠阻尼状态，故此仅分析 情况。同之前一致，方程的完整解为瞬态部分和稳态部分的叠加。忽略动态项，可以获得稳态时方程为：

稳态解为：

阶跃信号激励下的完整解为：

初始条件为： 时 ，带入振动方程可以得到：

绝大部分情况下，我们只研究零状态响应，此时 ，这样得到：

则方程的解为：

其中

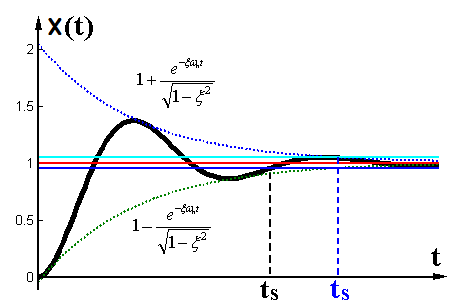
几个关键的指标量：

1）峰值时间

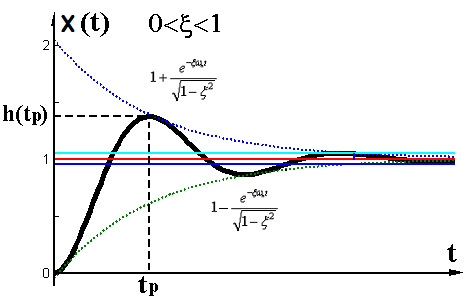
系统瞬态振动波峰对应的时间为：

当 时，对应的时间称之为峰值时间，此时：

2）超调量

峰值超过稳态值的比例称为超调量，计算如下：

超调量只跟阻尼比有关，随阻尼比的变化情况如下图所示：

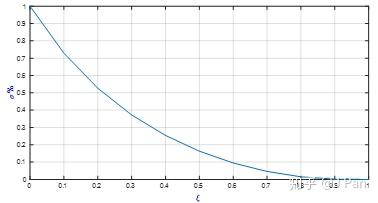
3) 调节时间

响应幅值与稳态值只差比例在0.05以内时对应的时间称为调节时间。

调节时间计算如下：

3.4 有阻尼受迫振动（冲击响应）

单位冲击响应的微分方程为：

由于单位冲击函数是单位阶跃函数的导数，故其时域响应也可以认为是单位阶跃响应的导数（零状态下），即：

不同阻尼比下欠阻尼二阶系统的冲击响应曲线如下图所示。