

Tricks for Manipulating Probability
source link: https://towardsdatascience.com/tricks-for-manipulating-probability-470b7eb7dfd?gi=3a6a1a8f1d2d
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

Dexterity in probability is needed to solve the fundamental problems of machine learning and artificial intelligence. This blog aims at summing up together the various techniques applied in different probability problems to make calculations easier and, sometimes, even possible! This blog assumes a basic understanding of probability and expectations. A prior revision of the basics, therefore, might be helpful for further understanding of the blog.
Let us, quickly, overview the common inference problems in Machine Learning and their probabilistic equations. We shall not go into the details about the problems. This list is supposed to act as a refresher and not a guide.
Evidence Estimation :
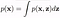
Moment Computation :
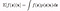
Parameter Estimation :
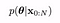
Prediction :

Hypothesis Testing :
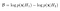
If you are unaware of some of these applications, don’t worry. It is not the focal point of the upcoming discussion but rather stresses the diverse domain of probabilistic modelling in ML. So, without any delay, let’s dive into the manipulation techniques for the above probability problems.
-
Identity Trick :
This transforms an expectation of f(x) w.r.t. a distribution p(x), into an expectation of g(x; f) w.r.t. distribution q(x). It’s a very simple trick yet very powerful. In many scenarios, computing expectation w.r.t. p(x) is difficult. So, we introduce a distribution q(x), which is mathematically convenient for us and transform the expectation as shown:

Application:
Let’s see a real problem from ML domain using this trick.
Evidence calculationin Bayes’ formula is an intractable problem in multidimensional variables. In Generative Models, calculating p(x) is a prime objective. Here, x is a sample, z is a latent variable and p(x|z) is the likelihood of observing the x given z. The equation given below is the marginalisation of the joint probability p(x, z) w.r.t. z.
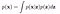
Gaussian Distribution.
We simply multiply and divide with q(z) and change the distribution for the expectation to q(z).


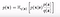
Conditions :
- q(z) > 0, when p(x|z)p(z) ≠ 0
- q(z) is known or is easy to handle.
We can proceed further and compute the expectation using the Monte Carlo
Sampling Methods as q(z) is easy to sample from. This is shown as :
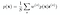
where,
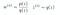
Note: We will discuss another method to solve this problem in Bounding Trick.
Identity Trick elsewhere:
- Manipulating stochastic gradients.
- Derive probability bounds.
- RL for policy correction.
2. Bounding Trick :
This trick comes from ‘convex analysis’ in which we bound the integral to be computed. One of them is Jensen’s Inequality,

In most of the ML problems, we use logarithms as the function f, because of their additive nature and strict concavity.
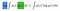
Other Bounding Tricks:
- Fenchel Duality.
- Holder’s inequality.
- Monge-Kantorovich Inequality.
An application appears in Evidence Lower Bound (ELBO) estimation in Variational Inference. Instead of using the Monte Carlo estimation of Evidence Calculation in the first trick, we will use Jensen’s Inequality to find a lower bound to optimise.
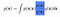
Taking the log and using Jensen’s inequality,
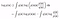
The RHS is the Variational Lower Bound, where
- The first term is the reconstruction loss.
- and the second term is the KL Divergence between the introduced approximate family of distribution over the latent variable, q(z) and the original p(z).
The first term takes the forms of l2 loss or cross-entropy loss depending upon the distribution of p(x|z) and the problem can be optimised using the Expectation Maximisation (EM) algorithm.

3. Density Ratio Trick:
Often, when we need a ratio of the probability densities, a naive way to calculate it is by computing both and then taking the ratio. This trick says that the ratio of two probability densities can be computed using a classifier which uses samples drawn from the two distribution. It is given by the following equation where p*(x) and q(x) are the two probability distributions and p(y=1|x) & p(y=-1|x) is the classifier.
Note: p* and p are not related. (Sorry for the notation abuse).


Let’s go through its derivation and find out the fundamentals of its working.
Create a dataset by combining samples from both the distributions {shown as ‘Combine data’} and assign +/- 1 as labels to denote the distribution {shown as ‘Assign labels’}. Now, in an equivalent setting, we can define our original distributions, p*(x) and q(x), as a conditional probability p(x|y) over the combined dataset {shown as ‘Equivalence’}.

Recall Bayes’ Rule which is here applied on both conditional distribution p(x|y=1) and p(x|y=-1) as shown below :

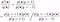
Note:A balanced dataset is created so that p(y=+1) equals p(y=-1). Therefore, it further simplifies as:

Density Ratio Trick elsewhere:
- Generative Adversarial Networks (GANs).
- Noise contrastive estimation.
- Two-sample testing.
Next, we look at the tricks used in manipulating the gradients of expectation of some function f.
Below is the most common gradient problem appearing in statistical science. If the distribution q(z) is simple and the integral is 1-D, expectation can be calculated and, hence, its gradient too. But, in a general framework, we can not calculate the expectation in closed form. Therefore, calculating its gradient becomes a non-trivial problem.
Here, Φ and θ are the parameters of q(z) and f(z) respectively.

Expressing the expectation into its integral form, we can see there are 2 ways to approach this gradient estimation:
- Differentiate the density q(z) : (Score-function estimator)
- Differentiate the function f(z) : (Pathwise estimator)
We will see, in detail, how both methods work and also work out an algorithm from RL as an example to get the intuition. In the example, we will formulate the above gradient estimation problem and solve it using our tricks.
Before that, these are the typical areas in which the above problem appears:
- Generative models and inference.
- Reinforcement learning and control.
- Operation research.
- Monte Carlo Simulation.
- Finance and asset pricing.
- Sensitivity estimation.
4. Log-Derivative Trick :
The first approach is to differentiate the density q(z), also called Score Function Estimator.
What is a ‘score’ in statistics?
The score (or informant) is the gradient of the log-likelihood function log( L(θ) ) w.r.t. the parameter vector θ (see wiki ).
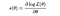
So, in our case, the trick is given by:

(Here, ϕ is the parameter, q is the likelihood function, and the gradient is w.r.t. ϕ )
Properties of the score function:
1. The expectation of the score function is 0. (Easy to prove. Hint: Jensen’s Inequality)

2. The variance of score function is given by the Fisher Matrix. (Just a useful property)

Let us find out how the above trick is used to solve the problem of stochastic optimisation.
In the figure given below,
1. The gradient is w.r.t. ϕ and the order of integration and gradient can be interchanged.
2. The gradient of q(z) is taken and identity trick is applied by multiplying and dividing with q(z) .
3. Log derivative trick comes into play.
4. The gradient of the shown expectation is transformed into an expectation of the shown function.
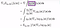

Note that we introduce a constant c which does not change the equation using the property “expectation of the score function is 0”. But subtracting a calculated constant c from f(z) reduces the variance of the gradients.
Now, we are ready to derive the Vanilla Policy Gradient in Reinforcement Learning.
Let us look at some definitions used in the derivation:
- A trajectory is a sequence of states and actions in the world.

Here, s and a denote state and action at any time t, respectively.
- The goal of the agent is to maximise some notion of cumulative reward over a trajectory, known as a return.
- One kind of return is the infinite-horizon discounted return , which is the sum of all rewards ever obtained by the agent but discounted by how far off in the future they are obtained. This formulation of reward includes a discount factor γ ∊ (0,1):
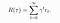
- Another kind is the finite-horizon undiscounted return , which is just the sum of rewards obtained in a fixed window of steps. We will use this in our derivation.
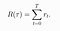
- A policy π is a rule used by an agent to decide what actions to take. It may be stochastic. The π in the below equation signifies the distribution of probability over actions in a given state. We often denote the parameters of such a policy by θ ,
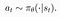
- Let’s suppose that both the environment transitions P and the policy π are stochastic. In this case, the probability of a T -step trajectory given the policy π is:
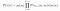
- The Log-Derivative Trick :
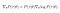
- The log-probability of a trajectory is just :
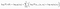
- The gradient of the log-probability of a trajectory is thus :

- Note that the environment has no dependence on θ , so gradients of initial state probability ρ and transition probability P are zero.
- The expected return is denoted by:

The goal in RL is to select a policy which maximises the expected return J(π) when the agent acts according to it. The central optimisation problem in RL can then be expressed by :

where, π* is the optimal policy.
We would like to optimise the policy by gradient ascent, like

The gradient of the policy performance, ∇J(π) , is called the policy gradient. The algorithms that optimise the policy in this manner are called policy gradient algorithms. The key idea underlying any policy gradient is to push up the probabilities of actions that lead to a higher return , and push down the probabilities of actions that lead to a lower return until you arrive at the optimal policy .
The derivation is given below (image snippet taken from Spinning Up RL). I highly recommend going through this resource to all RL practitioners. Link here .
This is an expectation, which means that we can estimate it with a sample mean. If we collect a set of trajectories D = {τ}, the policy gradient can be estimated with
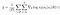
This brings us to our last trick,
Reparametrisation Trick :
You may have encountered this trick while dealing with Variational AutoEncoders. This is how it is performed in a general framework:Any distribution can be expressed as a transformation of other distributions. One example of this is the Inverse Sampling method, which says that all uniform distributions can be transformed into inverse CDF of the distribution we are interested in (see wiki ). In general, a distribution p(z) can be transformed into another distribution p( ε ) as follows:

Coming back to the second method of stochastic optimisation, we have pathwise estimator or reparametrisation trick. This time we will manipulate f(z).

Note that z is sampled from q(z). We introduced p( ε ) and a function g defined by the above equation. Now, substituting for z in our problem (given by below equation), we have
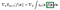


Both of the above methods help in converting the gradient of expectation into an expectation of some gradient which can further be approximated or efficiently calculated using Variational method or Monte Carlo method.
This is all for manipulating probabilities. I hope that the next time when you encounter your probability problem, you will be equipped with these tricks.
This is my first blog. Any feedback will be highly appreciated. I sincerely recommend going through the references for a better and more comprehensive understanding. If you did make it up till here, thanks a lot!
References :
[1] Advanced Deep Learning and Reinforcement Learning by DeepMind.
[2] Spinning Up RL by Open AI.
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK