How Big Is The Number — Tree(3)

Once upon a time, I was so naive and persistent that I counted all natural numbers up to one thousand in one go. That’s a record I never attempted to break, and hopefully won’t in near future. I mean, as a kid that number meant a great deal to me, and it can be quite a big number depending on the context.

So, I’m curious about what a big number means to you — is it a million, a billion, a googol, or a googolplex?

But if you are thinking about infinity, it is not fair. Infinity ain’t a real number, it’s a concept of an unfathomable idea without any end!

Alright, let’s play a game in which you are given three different seeds or nodes colored as red, black and green.

The idea is to build trees, as in graph theory, from these nodes such that the first tree would contain a single node, the second tree would have a maximum of two nodes, the third one would contain at most three nodes, and so on.

In this sequence, any particular tree must not contain its respective previous trees. Here, ‘ contain ’ emphasizes that two trees possessing similar nodes have also preserved their nearest common ancestors. Mathematically speaking, the smaller tree is said to be inf-embeddable within the larger one.

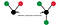
The above two trees cannot be present in the sequence since the left-tree is inf-embeddable within the right-tree.

In the above case, the trees are valid since the similar nodes share a distinct nearest common ancestor.

Let us consider another example to drive the point home:

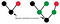
You may think that the above two trees are quite distinct. However, the opposite is true. By taking similar nodes into account, their respective nearest common ancestor turns out to be the same too!

Before moving on, let’s summarize the constraints:

• The nth tree should contain at most n nodes.
• All the previous ( n - 1 ) trees should not be inf-embeddable within the nth tree.

I hope you’ve understood the rules. So, let’s begin the game:

How many maximum possible trees can you construct before encountering a tree which always contains a previous tree?

Let us assume that we have only one kind of node at our disposal e.g. black. Hence, the number of trees we can build is one . Because the second tree would always contain the first tree owing to the presence of only one kind of node.

By defining a function for this game, TREE(k) ∀ k ∈ [1, n] where ‘ k ’ corresponds to the number of different kinds of nodes, we can state that TREE(1) = 1.

Similarly, by taking two different nodes e.g. red and black we can have three possible trees as shown below:

Any other variation would yield a lesser number of trees. Hence, in mathematical terms, TREE(2) = 3.

Now, how many such trees are possible when we consider three different nodes?

…take out a piece of paper and give it a shot!

Introducing TREE(3)

Have you ever encountered a calculation so big that you had to give up? Well, you can spend your entire life solving for TREE(3) and you won’t even come anywhere near to its actual value. TREE(3) is so gargantuan, so incomprehensibly massive, that no human can ever visualize it, understand it, or conceptualize it.

Even If you try to grasp the number of digits that constitutes TREE(3), or the number of digits of the number of digits in TREE(3) — your head would still collapse into a black hole because there’s a certain maximum limit of entropy that can be stored into your head.

You see, the smallest possible volume in our universe is 4.22 x 10^-105 cubic meters. This is known as Planck volume. Theoretically, if we wanted to fit every digit of TREE(3) in such infinitesimally small volume, we’d still run out of space in the universe. Hence, we can never unfold TREE(3) in our observable universe let alone this article.

At least, we know that TREE(3) is finite and can be proved even with the help of finite arithmetics. However, the amount of time it would take to prove the finiteness of TREE(3) is so large that the universe will come to an end way before concluding the proof.

Harvey Friedman, a mathematician at Ohio State University came up with a way to determine how many ‘symbols’ it would take to prove TREE(3) is finite. Even the number of symbols is exceedingly large. It is expressed as 2↑↑1000 in which ‘↑’ corresponds to a type of recurring exponential function. In this case, it would be 2 to the power 2 to the power 2… one thousand times.

In an episode of Numberphile, Tony Padilla who is an associate professor at The University of Nottingham came up with a thought experiment — suppose it takes one Planck time i.e. 5.39 × 10^-44 seconds to work through each symbol, then for a person who started the proof at the time of big bang, could he/she ever be able to finish it?

According to the Poincaré recurrence theorem, the answer is no. The theorem states that certain systems will, after a sufficiently long but finite time, return to a state very close to their initial state. If we were to believe that the entropy of our universe is finite, then the universe would eventually reset itself long before the proof ever materializes.

In a nutshell, if we use finite arithmetics we can never be able to prove physically that TREE(3) is finite. For practical proof, we need advanced techniques such as transfinite arithmetic and ordinal numbers .

TREE(3) actually came from Kruskal’s tree theorem and it is far far bigger than Graham’s number . In fact, Graham’s number is practically equivalent to zero when compared to TREE(3). The one thing that surprises me most is the colossal jump from TREE(2) to TREE(3). I can only wonder in awe what secret does TREE(4) and above holds! :cold_sweat:

Conclusion

Mathematics, as I’ve known, is a profoundly beautiful construct that constantly challenges the human imagination. And TREE(3) is one of those abstract ideas that we can never be able to comprehend yet math shows us it exists!