Introduction to Principal Component Analysis (PCA) — with Python code

Introduction to Principal Component Analysis (PCA) — with Python code

Introduction to PCA — The Why, When and How

Motivation

Imagine a text data having 100000 sentences. The total number of unique words in the text is 10000 (vocabulary size). If each sentence is represented by a vector of length equal to the vocabulary size. In this vector of length 10000, each position belongs to a unique word. For the vector of our sentence, if a certain word occurs k times, the value of the element in the vector corresponding to the index of this word is k . For every other word in the vocabulary not present in our sentence, the vector element is 0. This is called one-hot encoding.

Now, if we create vectors for each of these sentences, we have a set of 100000 vectors. In a matrix form, we have a 100000*10000 size matrix. This means we have 10⁹ elements in our matrix. In python, to get an estimate of the memory occupied,

import numpy as np
import sys
sys.getsizeof(np.zeros((100000,10000)))
>>> 8000000112

The number, in bytes, translates to 8000 megabytes.

What if we are able to work on a smaller matrix, one having fewer but more important features. Say, a few 100 features that capture most information about the data. Having more features is usually good. But more features often include noise too. And noise makes any Machine Learning algorithm less robust, especially on small datasets (read about the curse of dimensionality to know more). Moreover, we would save 100–1000 times the memory we consume. This is important when you deploy applications to production.

With this aim, let’s discuss how PCA helps us solve this problem.

Variance as Information

In Machine Learning, we need features for the algorithm to figure out patterns that help differentiate classes of data. More the number of features, more the variance (variation in data) and hence model finds it easy to make ‘splits’ or ‘boundaries’. But not all features provide useful information. They can have noise too. If our model starts fitting to this random noise, it would lose its robustness. So here’s the deal — We want to compose m features from the available feature space that give us maximum variance. Note that we want to compose and not just select m features as it is.

Mathematically Speaking

Say a data point is represented by a vector x and has n features originally.

vector x

Our job is to transform it into a vector z , having fewer dimensions than n , say m

vector z

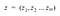
This happens through a Linear Transformation . Specifically, we multiply a matrix to x that maps it to an m- dimensional space. Consider a matrix W of size n*m . Using W , we wish to transform x to z as —

PCA transformation. Wt is the transpose of W

A simple interpretation of the above equation — Suppose you have an original data frame with columns —

Original Dataframe

After PCA, if we select, say 3 components, the data frame looks something like —

Where,

c1,c2,.. and d1, d2,… are scalars. W matrix is

W — a 5*2 matrix

Consider an example diagram below. The axis pointing northeast has more spread covered along its direction. Then the second most ‘covering’ axis points northwest.

Image credits: https://i1.wp.com/enhancedatascience.com/wp-content/uploads/2017/05/PCA1.png?resize=629%2C424

How to get W?

The above description is good enough for a small talk about PCA. But if you are curious about the calculation of W, this section is for you. You may skip it if you aren’t interested in the Math.

We discussed that PCA is about computing axes along which variance is maximized. Consider a single axis w , along which we wish to maximize the variance. Mathematically,

To calculate variance, we need mean. In statistics, it is better put as expectation, denoted by E. Expectation of a random variable is its mean. In our case we denote expectation of our original features x as μ. For our transformed features, z our expectation is wt* μ (see picture below)

If you are confused, refer the equation below, and take mean on LHS and RHS

matrix multiplication is commutative

Let mean of transformed features be

The variance of a sample of a random variable z is given by,

Expressed in terms of expectation and taking w out of the expectation operation (since it is a constant and not dependent on z )

Turns out, the variance of z is just wt*covariance of x (sigma) *w . Covariance is the variance of a multi-dimensional random variable, in our case, x . It is a square matrix of size k*k , where k is the dimension of x . It is a symmetric matrix . More on covariance matrix

Before we maximize the variance, we impose an important condition on the norm of our w matrix. The norm should be 1

Norm = 1

Why? Otherwise, the easy way of maximizing variance is by just increasing the norm and not re-aligning the principal axis in a way that maximizes the variance. This condition is included using a Lagrange multiplier

If we differentiate the above expression, we get —

Take a look at the last expression. Covariance matrix multiplied by w is equal to a scalar alpha multiplied by w . This means, w is the eigenvector of the covariance matrix and alpha is the corresponding eigenvalue . Using this result,

var(z) is the eigenvalue

If var(z) is to be maximized, then alpha has to be the largest of all eigenvalues. And the corresponding eigenvector is the principal component

This gives us the first principal component along which the variance explained is maximum compared to any other component. The above was the derivation for the first axis. Other axes are derived similarly. The point was to go a little deep in the math behind PCA.

Enough about the Math! Show me the code

The dataset we use is Coursera’s course reviews which is available on Kaggle . The code for this exercise is available on my GitHub repo.

As the name says, it consists of reviews (sentences) and ratings (1,2,3,4,5). We take 50,000 reviews, perform cleaning and vectorize them using TF-IDF .

TF-IDFis a scoring method that assigns a score to each word in the sentence. The score is high if the word does not commonly occur in all the reviews but occurs frequently overall. For example, the word course occurs frequently, but it occurs in almost every other review. So TF-IDF score for that word would below. On the other hand, the word poor occurs frequently and is specific to only negative reviews. So its score is higher.

So for every review, we have fixed length TF-IDF vector. The length of the vector is the size of the vocabulary. In our case, the TF-IDF matrix is of size 50000*5000. Moreover, more than 99% of the elements are 0. Because if a sentence has 10 words, only 10 elements of the 5000 will be non-zero.

We use PCA to reduce the dimensionality. But how to decide the number of components to take?

Let’s look at the plot of variance explained vs the number of components or axes

Variance explained vs the number of components

As you see, the first 250 components explain 50% of the variation. First 500 components explain 70%. As you can see, the incremental benefit diminishes. Of course, if you take 5000 components, the variance explained will be 100%. But then what’s the point of doing PCA?