统计学基础之假设检验

假设检验的基本概念

假设检验（Hypothesis Testing）是一种统计决策理论的方法，它利用观察得到的数据，对某个统计假设进行检验，以判断该假设是否合理。

在假设检验中，首先会提出两个对立的假设：原假设（Null Hypothesis，通常用H0表示）和备择假设（Alternative Hypothesis，通常用H1或HA表示）。原假设通常代表了一个默认的立场或者观点，备择假设则通常代表了研究者希望证明的立场或者观点。接下来的步骤是根据收集到的样本数据，选择适当的统计方法并计算出一个检验统计量，然后根据这个统计量和预先设定的显著性水平，决定是否拒绝原假设。如果检验统计量落在拒绝域（即，它对应的概率值小于显著性水平），那么我们就拒绝原假设，接受备择假设，否则我们就接受原假设。

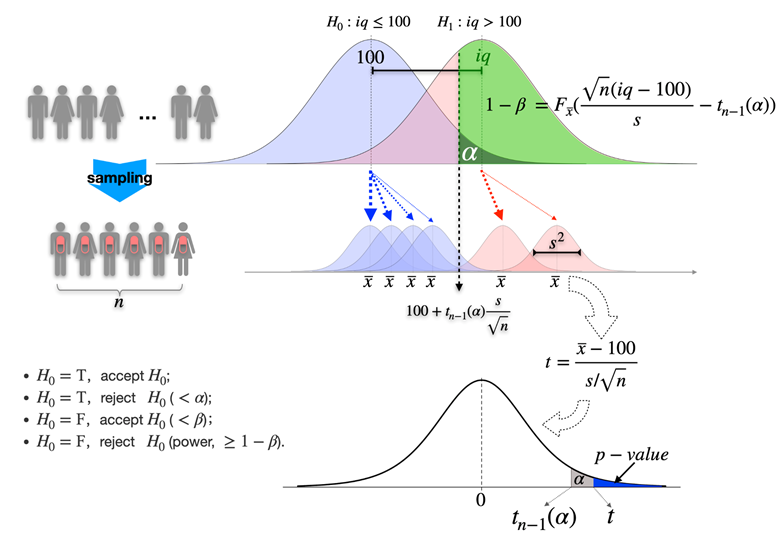
在假设检验中，我们也需要考虑到检验的错误。类型I错误是指我们错误地拒绝了真实的原假设；类型II错误是指我们错误地接受了假的原假设。在实际应用中，我们通常需要权衡这两种错误，根据具体情况设定一个合适的显著性水平（也称为错误的容忍度或置信水平），以控制犯错误的概率。

假设检验是统计学中一个重要的工具，其主要目的是帮助我们根据样本数据对总体参数做出推断。以下是进行假设检验的主要原因：

• 确定观测结果的统计显著性：假设检验可以帮助我们判断观察到的数据或结果是否是由随机变化造成的，还是由一些特定的因素造成的。通过假设检验，我们可以确定结果的统计显著性，即结果不太可能仅仅由随机因素产生。
• 帮助决策：在商业和研究中，我们经常需要根据数据做出决策。假设检验提供了一种基于数据推断总体情况的方法，可以帮助我们做出更有依据的决策。
• 验证理论：在科学研究中，假设检验常常用来验证理论假设。例如，我们可以通过假设检验来检查某种药物是否有效，一种教学方法是否优于另一种方法等。
• 控制风险：假设检验中的显著性水平和功效可以帮助我们控制错误的概率，从而控制决策的风险。

总的来说，假设检验的目的和意义在于，它提供了一种基于样本数据推断总体状况，验证科学假设，做出决策的科学方法。

如何向小学生解释什么是假设检验？

假设检验可以理解为一种“猜一猜”游戏。假设你有一个神秘的魔法盒子，你想知道这个盒子里有没有玩具。你猜，可能有玩具，也可能没有玩具。这就像假设检验中的两个“假设”：一个叫“零假设”，就是盒子里没有玩具，一个叫“备择假设”，就是盒子里有玩具。

然后你可以摇摇盒子，听听里面有没有动静。如果你听到了里面有东西在滚动的声音，那么你可能就会认为“嗯，盒子里应该有玩具”。这就像假设检验中的“检验统计量”，帮助我们做出判断。

但是，这个声音可能是玩具，也可能是别的东西，比如石头或者硬币。所以，即便我们听到了声音，也不能百分之百确定盒子里一定有玩具。我们只能说，如果盒子里没有玩具，那么我们能听到这样的声音的可能性很小。这就像假设检验中的“P值”。

如果这个可能性非常非常小（比如小于5%），那么我们就认为我们最初的猜测“盒子里没有玩具”可能是错的，我们更愿意相信“盒子里有玩具”。这就是假设检验的结果。

这就是假设检验的基本过程：先提出两个相反的假设，然后收集证据，最后根据证据来判断哪个假设更有可能是真的。但需要记住的一点是，无论我们的判断多么有信心，都可能存在一定的错误。因为，除非我们打开盒子看看，否则我们永远不可能完全确定盒子里是否真的有玩具。

假设检验的步骤

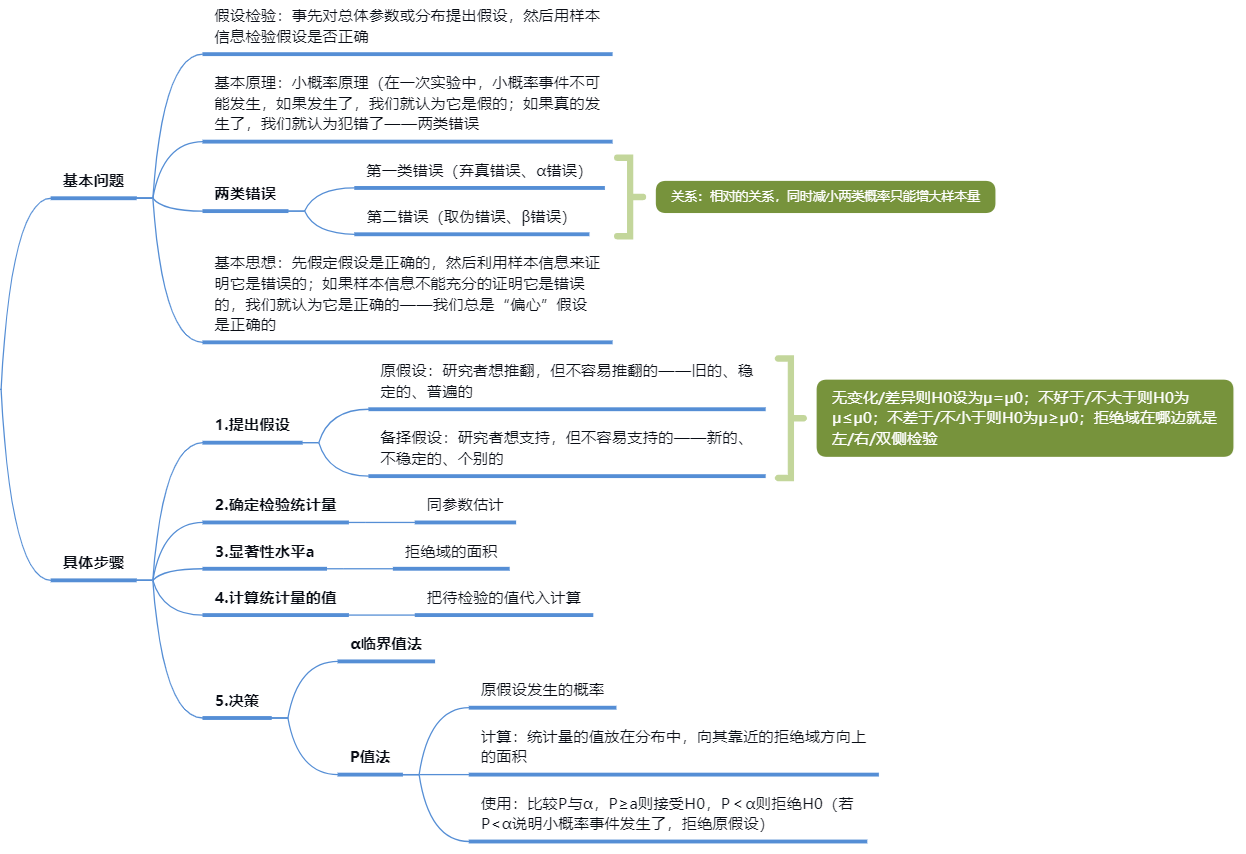
假设检验的基本步骤包括以下几个：

• 提出假设：设立原假设（H0）和备择假设（H1或Ha）。原假设是要进行检验的假设，通常表示的是观察的现象由随机因素引起，或者说研究者所主张的特性不存在。而备择假设则是研究者想要证明的主张。
• 选择合适的检验统计量：根据问题的具体情况和所使用的数据类型，选择一种适合的统计方法，例如t检验，卡方检验等。然后，计算检验统计量的值。
• 确定显著性水平和拒绝域：显著性水平（α）是你愿意冒的出现第一类错误（弃真）的风险。一般取05或0.01。拒绝域是所有导致原假设被拒绝的样本观察值构成的范围。
• 判断检验统计量落在接受域还是拒绝域，得出结论：如果检验统计量的值落在拒绝域内，那么我们就拒绝原假设，接受备择假设；否则，我们就接受原假设，拒绝备择假设。
• 解释结果：对于结果进行解释，注意这里的解释结果并不能完全确定一个事实，只能说在一定的置信水平下，我们有足够的证据拒绝或者无法拒绝原假设。

以上就是假设检验的一般步骤，但是具体实施的时候，可能会根据研究问题的不同，统计方法的不同有所差异。

如何设立原假设和备择假设？

在假设检验中，原假设和备择假设是至关重要的。以下是如何设立这两种假设的一些指导原则：

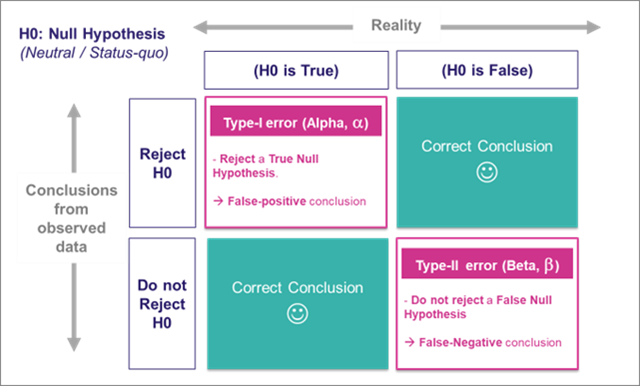
• 原假设（Null Hypothesis，H0）：原假设通常是研究者想要反驳的假设，也就是说，如果你的研究目标是证明某种效应存在，那么原假设就应该设定为这种效应不存在。例如，如果你想证明某种药物可以有效治疗某种疾病，那么原假设就应该设定为这种药物不能有效治疗这种疾病。
• 备择假设（Alternative Hypothesis，H1或Ha）：备择假设通常是研究者想要证明的假设，也就是说，如果你的研究目标是证明某种效应存在，那么备择假设就应该设定为这种效应存在。在上述的药物实验中，备择假设就应该设定为这种药物可以有效治疗这种疾病。

在设立原假设和备择假设时，值得注意的是，假设检验的结果并不能证明原假设或备择假设是真实的，它只能告诉我们，基于我们收集到的数据，我们有足够的证据拒绝原假设，或者我们没有足够的证据拒绝原假设。

如何选择检验统计量？

根据所研究的问题和数据类型（例如，均值、比例或差异等），选择一个合适的统计量来度量样本观察值与原假设之间的偏差。这个统计量应当在原假设成立的情况下有一个已知的概率分布。

选择检验统计量的过程取决于你的研究问题、你想要检验的假设以及你的数据类型。以下是一些常见的情况和相应的检验方法：

• 如果你想要比较两个独立样本的均值，你可能会选择独立样本t检验。如果样本是配对的，你可能会选择配对样本t检验。
• 如果你想要比较两个或多个样本的方差是否相等，你可能会选择F检验。
• 如果你想要检验两个变量之间是否存在相关性，你可能会选择皮尔逊相关性检验。
• 如果你想要检验分类变量之间是否独立，你可能会选择卡方独立性检验。
• 如果你想要检验某个样本的分布是否符合某一特定的理论分布（如正态分布），你可能会选择K-S检验。

以上只是一些常见情况下的处理方法，实际上，选择哪一种检验统计量是取决于你的研究设计和数据情况的。在选择检验统计量时，你也需要考虑你的数据是否满足这些检验的前提假设。例如，t检验和F检验都假设数据服从正态分布，如果你的数据明显偏离正态分布，那么你可能需要选择其他的检验方法，或者对数据进行转换。

如何确定显著性水平和拒绝域？

显著性水平（alpha，通常以α表示）是你愿意接受的错误拒绝原假设（即实际上原假设为真，但我们的分析结果却拒绝了原假设，这是第一类错误）的最高概率。常见的显著性水平有0.05和0.01，取哪个值取决于你的研究领域和你个人对错误的容忍度。

拒绝域是所有导致原假设被拒绝的样本观察值构成的范围。它与显著性水平和备择假设密切相关。如果是双尾检验（即备择假设是”不等于”类型），那么拒绝域就会出现在分布的两个尾部；如果是单尾检验（即备择假设是”大于”或”小于”类型），那么拒绝域就会出现在分布的某一个尾部。

具体的拒绝域的确定，通常是通过查阅相应分布的临界值表（如t分布表，z分布表，卡方分布表等），找到与你设定的显著性水平对应的临界值，然后这个临界值就是拒绝域的边界。如果你的检验统计量的值落入了这个范围，那么你就拒绝原假设。否则，你就不能拒绝原假设。

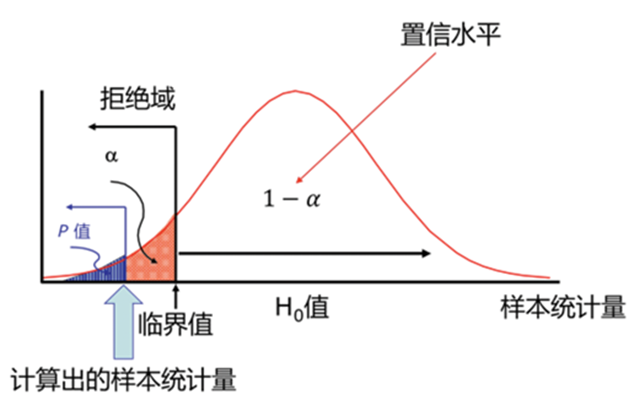
p-value即为拒绝域，我们各种检验最终都是求拒绝域的大小，当拒绝域大于我们设置的阈值(显著性水平)，那么置信水平就没有那么大了，那么就要放弃原假设，改而支持备择假设了。

P值：在原假设为真的情况下，观察到的样本统计量或更极端值出现的概率。P值越小，拒绝原假设的证据越强。

• 如果P值小于或等于显著性水平α，那么拒绝原假设，认为结果具有统计学上的显著性，支持备选假设。
• 如果P值大于显著性水平α，那么不拒绝原假设，认为没有足够的证据支持备选假设。

假设检验相关概念

在统计学中，P值 (p-value) 是进行假设检验时使用的一个重要概念。它表示在原假设成立的前提下，出现观察到的数据或更极端情况的概率。

假设检验的过程通常开始于设立一个原假设，这个假设通常代表了一个“无效”或“无差异”的情况（例如，两组数据的均值相同）。然后我们使用收集到的数据来计算一个检验统计量，这个统计量反映了观察到的数据与原假设之间的差异程度。最后，我们根据这个统计量的值来计算P值。

如果P值很小（通常是小于某个预设的阈值，如0.05或0.01），那么我们就认为观察到的数据与原假设的差异是“显著”的，所以我们有足够的证据拒绝原假设。反之，如果P值较大，我们则认为没有足够的证据拒绝原假设。

简单来说，P值越小，我们观察到的数据支持原假设的可能性就越小。因此，P值可以被看作是我们的数据支持原假设的“强度”的度量。

然而，值得注意的是，P值并不能告诉我们备选假设成立的概率，也不能告诉我们原假设错误的概率。它也不能提供我们关于效应大小（即原假设和观察到的数据之间差异的程度）的信息P值（概率值）是在统计假设检验中一个非常重要的概念。它提供了一个量化的度量，用于在给定的统计模型和原假设（H₀）下评估观察到的数据（或更极端情况）的概率。简而言之，P值可以帮助我们理解，在原假设为真的情况下，观察到当前样本数据或更极端数据的可能性有多大。

P值的定义

P值：在原假设为真的条件下，得到当前观测值或更极端情况的概率。它是一个介于0和1之间的数值，用于衡量数据与原假设之间的不一致程度。

解读P值

• 低P值（通常≤05）意味着在原假设为真的情况下，观察到的数据（或更极端的数据）出现的概率低。这通常被解释为有足够的证据拒绝原假设。换句话说，观察到的数据与原假设之间存在显著差异。
• 高P值意味着观察到的数据在原假设为真的情况下出现的概率高，表明数据与原假设之间没有显著差异，因此没有足够的证据拒绝原假设。

P值与显著性水平（α）

显著性水平α是在假设检验之前确定的阈值，通常设置为0.05或0.01，用于决定是否拒绝原假设。P值与α的比较是做出检验决策的关键。

• 如果P值 ≤ α，则认为观察到的结果（或更极端）在统计上是显著的，拒绝原假设。
• 如果P值 > α，则没有足够的证据在统计上拒绝原假设。

P值的误解

• P值不是观察到的结果发生的绝对概率，而是在原假设为真的条件下得到这些结果的概率。
• P值不是原假设或备选假设为真的概率。统计检验并不直接提供原假设为真或假的概率，而是提供了在原假设为真时观察到特定数据的概率。
• P值不是效应大小的度量。一个小的P值可能指示存在显著差异，但不告诉我们这个差异有多大。

结论

P值是假设检验中一个核心概念，它帮助我们量化观察结果与原假设之间的一致性。正确理解和解释P值对于作出正确的统计推断至关重要。记住，低P值并不一定意味着发现了实际意义重大的结果，还需要综合考虑研究背景、效应大小和其他相关证据。

由于“置信区间”是“区间估计”中的一个概念，而讲“区间估计”之前，得先介绍“点估计”。

点估计

“估计”是指用样本的数据估计全体的数据情况。之所以这么做，是因为很多时候，想全体采集数据太难了，又或者采集全体数据不现实，万一这个方案不好又推给全量用户会导致营收下降！所以必须抽样。

那么，直接用单回抽样数据值代表全体数据，就是所谓的“点估计”。

常见的点估计指标有2种：

• 人均值：比如经抽样得到的一个人群，这些人对某个图标按钮的人均点击次数是3次（按钮总点击次数 / 人群人数）。
• 转化率：比如经抽样得到的一个人群，这些人对某个转化页面中进入下一步的按钮的点击转化率为10%（按钮点击人数 / 页面浏览人数）。

但是，只使用一个抽样人群得到的数据值直接对总体进行估计是有问题的。哪怕每回抽样再随机，抽样对象不同，点估计值总会有细微差异，比如某按钮点击转化率指标，如果重复做5回随机抽样（抽5组人群分别计算），可能会得出5个不同的转化率，到底哪个转化率才能代表全体用户呢？为了解决这个问题，有了区间估计的做法。

区间估计

通俗地讲：区间估计是在点估计的基础上，给一个合理取值范围。

• 我们预计某个页面按钮的点击转化率为10%（这是进行点估计）
• 我们预计某个页面按钮的点击转化率在5%～11.5%之间（这是在进行区间估计）

使用一个数值范围来进行估计，我们对于总体的实际数值会不会落在这个范围内就变得更有把握了。

置信区间

在上述例子中，“8.5%～11.5% ”就称为置信区间，这很符合人们的常规理解：点估计的值很难 100% 准确，而使用一个数值范围则能使结论变得更加严谨。但这个范围又有多大可信度呢？人们用「置信水平」来衡量，即为：“我们有多大把握，实际数值会落在置信区间内。”

「置信水平」一般用（1-α）表示。如果 α 取0.05，则置信水平为 0.95，即 95% 的把握。将置信区间与置信水平连起来，完整的表达即为：“我们有 95% 的把握，该按钮曝光点击转化率的实际值会落在 8.5% 至 11.5% 之间。”

在统计学中，置信区间（Confidence Interval）是一种用来估计总体参数（例如总体均值或总体比例）的方法。置信区间提供了一个区间估计，表示总体参数有可能落在该区间内的概率。

以下是置信区间的关键概念：

置信水平

置信水平（Confidence Level）定义了置信区间的宽度。常见的置信水平有90%、95%和99%。例如，95%置信区间表示我们有95%的置信度，认为这个区间包含了总体参数。

置信区间的计算

置信区间的计算基于样本统计量（例如样本均值）和标准误差。对于均值的置信区间，可以使用以下公式：

置信区间 = 样本均值 ± Z分数 * 标准误差

其中，Z分数取决于所选择的置信水平。例如，对于95%的置信水平，Z分数通常取1.96。

解读置信区间

置信区间提供了关于总体参数的可能范围的估计。然而，需要注意的是，我们不能说有95%的概率参数在置信区间内，因为置信水平描述的是如果我们无限次重复抽样并计算置信区间，有多少比例的置信区间会包含总体参数。

例如，如果我们有一个95%的置信区间为[5,10]，我们不能说有95%的概率总体均值在5到10之间。我们只能说，如果我们不断重复抽样和计算95%的置信区间，那么大约95%的这些区间会包含真正的总体均值。

置信区间与样本大小

样本大小会影响置信区间的宽度。随着样本大小的增加，样本统计量的标准误差会减小，因此置信区间也会变窄。这意味着随着样本大小的增加，我们对总体参数的估计会越来越精确。

总的来说，置信区间是一种实用的统计工具，可以帮助我们理解总体参数可能的取值范围。然而，正确理解和解读置信区间需要对置信水平、置信区间的计算以及置信区间的解读有深入的理解。

显著性水平

显著性水平，通常用α（阿尔法）表示，是在统计假设检验中事先选择的标准，用来决定观察结果是否具有统计显著性。它定义了拒绝原假设的证据的强度，通常取0.05、0.01等值。例如，如果显著性水平设为0.05，这意味着我们愿意接受5%犯错误拒绝一个真实的原假设的风险（也就是犯类型I错误的概率）。

显著性水平与置信区间的关系

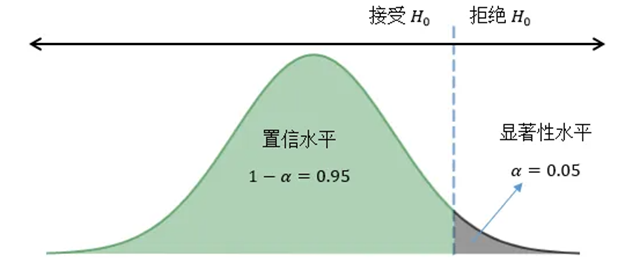
显著性水平和置信区间都与统计推断中的不确定性的量化有关，但它们应用于不同的统计过程和目的。

• 概念桥接：显著性水平主要用于假设检验中，用来判断样本数据是否提供足够证据拒绝原假设。而置信区间用于参数估计，提供了一个区间范围，表明总体参数很可能位于这个范围内。
• 数值联系：显著性水平α与置信水平（1-α）相互补充。例如，如果显著性水平为05（表示5%的风险水平拒绝真正的原假设），对应的置信水平为0.95（或95%），意味着我们有95%的置信度认为置信区间包含了真正的总体参数。显著性水平决定了在假设检验中拒绝原假设的临界值，而这个临界值直接影响到置信区间的计算结果。
• 应用差异：虽然它们都是统计分析中的关键概念，但显著性水平主要关注于“结果是否偶然发生”（即结果是否具有统计显著性），而置信区间则关注于“参数的可能范围是多少”。

综上，显著性水平和置信区间虽然在应用上有所不同，但它们都是统计推断的重要工具，相互之间存在联系，并且都是帮助我们理解数据背后总体特征的方法。正确理解和运用这两个概念对于进行科学研究和数据分析是非常重要的。

显著性水平与P值的关系

显著性水平，通常表示为α，是在进行假设检验之前设定的阈值，被用来判断观察到的数据是否具有统计显著性。它表示的是在原假设为真的情况下，犯第一类错误（拒真错误显著性水平（通常用α表示）和P值都是统计假设检验中的核心概念，它们之间有直接的关系和区别，下面是它们之间关系的详细解释：

• 显著性水平是在假设检验开始之前就设定的阈值，用来确定是否有足够的证据拒绝原假设。它代表的是在原假设为真的前提下，错误拒绝这个假设（即犯第一类错误，或称为“假阳性”）的最大可容忍概率。常用的显著性水平包括05（5%）、0.01（1%）等，其中0.05是最常见的选择。
• P值是在假设检验过程中计算得到的，它表示在原假设为真的情况下，观察到的数据（或更极端的情况）出现的概率。P值是一种条件概率，它告诉我们，在没有效应或差异存在的情况下（即原假设为真），得到当前观测结果或更极端结果的可能性。

显著性水平与P值的关系

在进行假设检验时，我们将计算出的P值与事先设定的显著性水平α进行比较，以决定是否拒绝原假设。

• 如果P值 ≤ α，表示在原假设为真的前提下，得到当前观测数据（或更极端）的概率非常小，因此我们有足够的证据拒绝原假设，认为结果具有统计显著性。
• 如果P值 > α，表示没有足够的证据拒绝原假设，即我们的观测结果可以在原假设为真的情况下合理地发生，因此我们保留原假设。

关键点

• 显著性水平α是我们事先设定的标准，而P值是基于观察数据计算得出的结果。
• 通过比较P值和显著性水平α，我们可以做出统计推断，即决定是否拒绝原假设。

显著性水平决定了结果被认为具有统计显著性的门槛。

类型I错误和类型II错误

在统计学中，类型I错误和类型II错误是两种在假设检验中可能出现的错误类型。它们与我们对检验结果的决策有关。

类型I错误（Type I Error）

类型I错误，也叫做假阳性错误，是指在原假设（null hypothesis）为真的情况下，错误地拒绝了原假设。换句话说，我们认为有足够的证据说明观察到的数据与原假设不一致，从而拒绝了原假设，但实际上原假设是正确的。

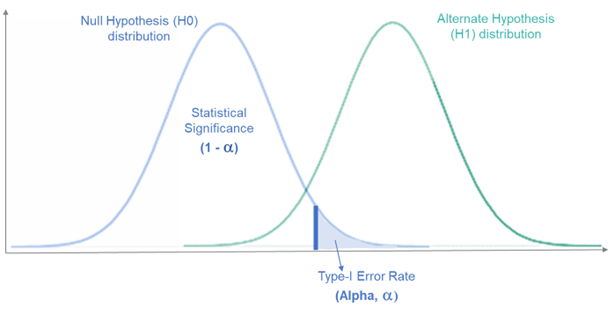
例如，假设我们进行一项药物试验，原假设是新药物无效。如果新药物实际上是无效的，但测试结果显示新药物有效，那么我们就犯了类型I错误。

类型I错误的概率由我们设定的显著性水平（通常表示为 alpha）决定。例如，如果显著性水平设为0.05，这意味着我们愿意接受5%犯类型I错误的风险。

类型II错误（Type II Error）

类型II错误，也叫做假阴性错误，是指在备择假设（alternative hypothesis）为真的情况下，错误地未拒绝原假设。也就是说，实际上我们应该拒绝原假设，因为备择假设是正确的，但我们没有这么做。

继续上面的药物试验的例子，如果新药物实际上是有效的，但测试结果显示新药物无效，那么我们就犯了类型II错误。

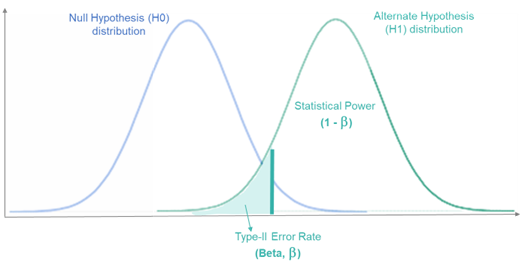
类型II错误的概率通常表示为 beta。统计学家通常会设定一个阈值，使得 beta 低于这个阈值。beta 的补数（1-beta）被称为测试的”功效”（power），表示正确拒绝原假设（即检测到效应）的能力。

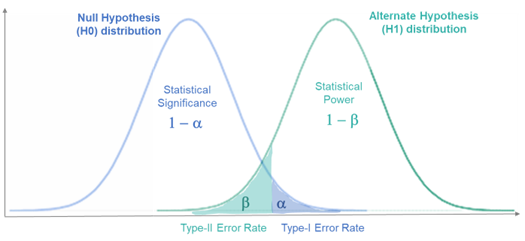
总的来说，类型I错误和类型II错误是统计决策中的两种潜在错误。统计学家会设定阈值，通过控制 alpha 和 beta，来平衡这两种错误的风险。同时，这也揭示了一个关键的统计事实，那就是我们必须接受在决策过程中存在一定的错误风险。

在实际的研究中，我们通常希望尽量降低这两种错误的概率，但往往会出现这两种错误之间的权衡。例如，如果我们希望降低第一类错误的概率（即提高检验的严格性），那么可能会提高第二类错误的概率（即降低检验的功效）。因此，如何选择合适的显著性水平以及如何设计和执行研究，以便在控制第一类错误的同时尽量降低第二类错误，是实际研究中需要考虑的问题。

单侧检验和双侧检验

在做假设检验时，我们需要根据研究问题和假设来确定是进行单侧检验还是双侧检验。

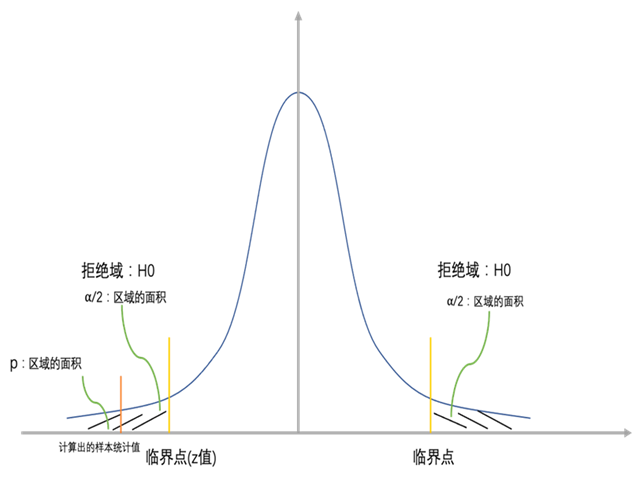
• 单侧检验（One-tailed test）：如果我们的研究假设是方向性的，比如我们想要检验某个参数是否大于（或小于）某个值，那么我们就进行单侧检验。在单侧检验中，我们只关注分布的一个方向（尾部）的极端情况。比如，如果我们想要检验男性的平均身高是否高于170cm，那么我们就进行大于170cm方向的单侧检验。
• 双侧检验（Two-tailed test）：如果我们的研究假设是非方向性的，比如我们想要检验某个参数是否不等于某个值，那么我们就进行双侧检验。在双侧检验中，我们关注分布的两个方向（两个尾部）的极端情况。比如，如果我们想要检验男性的平均身高是否不等于170cm，那么我们就进行双侧检验。

在进行假设检验时，选择单侧检验还是双侧检验取决于你的研究问题和假设，而不是你的数据。在确定了检验类型后，你需要根据检验类型来计算检验统计量的P值和确定拒绝域。

参数检验和非参数检验

参数检验和非参数检验是统计学中两种不同类型的假设检验方法：

• 参数检验：参数检验是基于对数据分布的一些假设进行的，例如假设数据服从正态分布，或者假设各组数据的方差相等等。参数检验的方法包括t检验、F检验（方差分析）和卡方检验等。参数检验的优点是在满足其假设的情况下，其结果的可靠性和效力都较高；但缺点是，当数据违反其假设时（例如数据严重偏离正态分布），参数检验的结果可能会不准确。
• 非参数检验：非参数检验并不基于对数据分布的任何假设，因此它可以适用于更广泛的情况，尤其是当数据不能满足参数检验的假设时。非参数检验的方法包括Mann-Whitney U检验、Wilcoxon符号秩检验和Kruskal-Wallis H检验等。非参数检验的优点是它对数据的要求较低，不管数据是否满足正态分布或等方差性，都可以使用非参数检验。但缺点是，由于没有利用数据分布的信息，非参数检验的效力（即发现实际效应的能力）通常低于参数检验。

选择参数检验还是非参数检验，主要取决于你的数据是否满足参数检验的假设，以及你对检验效力和健壮性的取舍。在实际研究中，如果数据满足参数检验的假设，通常会优先选择参数检验。如果数据不满足参数检验的假设，而且你也无法（或者不愿意）通过转换数据来满足这些假设，那么就可以选择非参数检验。

检验的功效

效力分析（Power Analysis）是统计学中的一种方法，用于确定研究设计是否有足够的能力来检测感兴趣的效应或差异。

在效力分析中，”效力”（power）是一个重要的概念。它被定义为在备择假设（alternative hypothesis）为真的情况下，正确拒绝原假设（null hypothesis）的概率。换句话说，效力是避免犯类型II错误（假阴性错误）的能力。效力的值范围在0到1之间，值越接近1，避免犯类型II错误的能力越强。

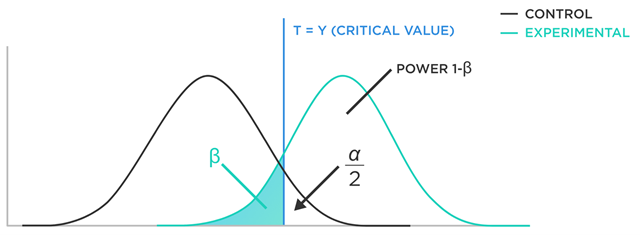
效力的大小受多个因素影响，包括：

• 样本大小：样本大小越大，检验的功效越高。因为样本大小增大可以使得我们对参数的估计更加精确，从而更容易发现实际的效应。
• 效应大小：效应大小越大，检验的功效越高。因为如果实际效应非常大，那么即使样本大小不大，我们也可能很容易地发现这个效应。
• 显著性水平：显著性水平越小，检验的功效越低。因为显著性水平越小意味着我们希望以更高的标准来避免犯第一类错误，这可能会导致我们更难以发现实际的效应。
• 检验类型：一般来说，参数检验的功效高于非参数检验。因为参数检验使用了更多的信息（如数据的分布信息），因此其发现实际效应的能力通常更强。

效力分析的主要应用包括：

• 确定样本大小：在研究设计阶段，我们可以通过效力分析来确定需要的样本大小，以确保有足够的能力检测到感兴趣的效应。
• 评估研究结果：如果一个研究发现没有统计显著性，我们可以通过效力分析来评估这是由于真的没有效应，还是由于研究的效力不足。

总的来说，效力分析是一个重要的统计工具，可以帮助研究者在设计和评估研究时做出更好的决策。

一般来说，功效的计算涉及到复杂的统计方法，并且需要使用统计软件进行。

使用Python进行效力分析

效力分析是在实验设计阶段，对实验的样本量，效应量，α水平（Type I error，第一类错误，即原假设为真时，我们却错误地拒绝了原假设）和功效（Power，1-β，即原假设为假时，我们正确拒绝原假设的概率）之间关系的分析。

在Python中，我们可以使用statsmodels库中的power模块来进行效力分析。以下是一个示例，计算在给定效应量、样本量和α水平下，检验的功效：

from statsmodels.stats.power import TTestIndPower

# 参数设定
effect_size = 0.8
nobs1 = 50
alpha = 0.05

# 初始化功效分析对象
power_analysis = TTestIndPower()

# 计算功效
power = power_analysis.solve_power(effect_size=effect_size, nobs1=nobs1, alpha=alpha)
print('Power: ', power)

同样，我们也可以使用statsmodels来计算达到期望功效所需的样本量。例如：

# 参数设定
effect_size = 0.8
alpha = 0.05
power = 0.8

# 计算所需样本量
nobs1 = power_analysis.solve_power(effect_size=effect_size, alpha=alpha, power=power)
print('Required sample size: ', nobs1)

以上就是在Python中进行效力分析的基本方法。

常见的假设检验方法

假设检验是统计学中的一种重要方法，主要用于推断总体参数。以下是一些常见的假设检验方法：

• t检验：用于比较两组观测值的平均值是否存在显著差异。常见的有单样本t检验、独立样本t检验和配对样本t检验。
• F检验：主要用于比较三个或更多个样本的方差或均值是否存在显著差异，包括单因素方差分析（One-way ANOVA）和多因素方差分析（Two-way ANOVA）。
• 卡方检验：主要用于比较观察频数与期望频数是否有显著差异，或者检验两个分类变量是否相关。
• Z检验：当样本量大于30且总体标准差已知时，用于比较样本均值与总体均值是否存在显著差异。
• Mann-Whitney U检验和Wilcoxon符号秩检验：主要用于非参数假设检验，比如两个独立样本或配对样本的中位数是否存在显著差异。
• Fisher精确检验：用于在样本量较小的情况下，比较两个分类变量的关联性。
• Levene检验和Bartlett检验：用于检验两个或多个样本的方差是否相等。

以上是常见的一些假设检验方法，每种方法都有其适用的场景和前提假设，选择合适的假设检验方法需要根据具体的研究问题和数据状况来定。

t检验（t-test）是统计学中常用的一种参数检验方法，用于检验两个样本均值之间是否存在显著差异。t检验假设数据服从正态分布，且一般认为它对小样本数据具有较好的鲁棒性。

t检验主要有三种类型：

• 独立样本t检验（Independent Samples t-test）：用于比较两个独立样本（比如，来自两个不同的实验条件或者两个不同的人群）的均值是否存在显著差异。
• 配对样本t检验（Paired Samples t-test）：用于比较同一组个体在不同条件下的均值是否存在显著差异。比如，想要比较某种药物治疗前后的病人健康状况。
• 单样本t检验（One-sample t-test）：用于比较单一样本的均值与某个已知的参考值（或理论值）是否存在显著差异。

在进行t检验时，首先要计算t统计量，然后根据t统计量的大小和自由度去查t分布表，得到对应的P值。如果P值小于事先设定的显著性水平（通常为0.05），那么我们就拒绝原假设，认为两个样本均值之间存在显著差异。

需要注意的是，虽然t检验对样本数据的正态性假设具有一定的鲁棒性，但如果样本数据严重偏离正态分布，或者两个样本的方差差异过大，那么t检验的结果可能会不准确，这时就需要考虑使用其他更为鲁棒的检验方法，如Mann-Whitney U检验等。

在Python中，使用scipy.stats库可以轻松实现t检验。以下是几种常见的t检验的Python示例。

单样本t检验

检验样本均值是否等于某一个已知值。例如，检验一个班级学生的平均身高是否等于全校的平均身高。

from scipy import stats
# 假设heights为班级学生的身高数据，school_mean为全校的平均身高
heights = [170, 168, 169, 171, 172, 173, 169, 170, 172]
school_mean = 170
t_statistic, p_value = stats.ttest_1samp(heights, school_mean)
print('t statistic:', t_statistic)
print('p value:', p_value)

独立双样本t检验

检验两个独立样本的均值是否相等。例如，比较男生和女生的平均身高是否有差异。

from scipy import stats

# 假设male_heights和female_heights分别为男生和女生的身高数据
male_heights = [175, 176, 178, 179, 180, 174, 176]
female_heights = [165, 166, 167, 168, 169, 166, 167]
t_statistic, p_value = stats.ttest_ind(male_heights, female_heights)
print('t statistic:', t_statistic)
print('p value:', p_value)

配对样本t检验

检验同一组样本在不同条件下的均值是否相等。例如，比较学生上学前后的体重差异。

from scipy import stats

# 假设weights_before和weights_after分别为学生上学前和上学后的体重数据
weights_before = [60, 62, 61, 63, 64, 62, 61]
weights_after = [62, 64, 63, 65, 66, 64, 63]
t_statistic, p_value = stats.ttest_rel(weights_before, weights_after)
print('t statistic:', t_statistic)
print('p value:', p_value)

这些都是最常见的假设检验。在使用这些检验前，记得先确认你的数据满足检验的前提假设（比如数据服从正态分布，各组样本独立等）

卡方检验（Chi-Square Test）是一种非参数检验的统计方法，广泛用于比较观测频数和期望频数，或者比较两个或多个分类变量之间的关联性。

卡方检验主要有两种类型：

• 卡方独立性检验（Chi-Square Test of Independence）：用于检验两个分类变量之间是否独立。例如，我们可以用卡方独立性检验来检验性别（男、女）和党派偏好（民主党、共和党、独立党）之间是否存在关联。
• 卡方拟合优度检验（Chi-Square Goodness of Fit Test）：用于检验观测频数和期望频数之间是否存在显著差异。例如，我们可以用卡方拟合优度检验来检验一个骰子的六个面出现的频率是否均等。

在进行卡方检验时，首先要计算卡方统计量，然后根据卡方统计量的值和自由度去查卡方分布表，得到对应的P值。如果P值小于事先设定的显著性水平（通常为0.05），那么我们就拒绝原假设，认为观测频数和期望频数之间存在显著差异，或者两个分类变量之间存在关联。

需要注意的是，卡方检验的适用条件是每个单元格的期望频数都要大于5，如果有太多的单元格期望频数小于5，卡方检验的结果可能会不准确。

在Python中，我们可以使用scipy.stats库的chi2_contingency方法来进行卡方检验，主要用于测试分类变量之间的独立性。下面是一个示例：

from scipy.stats import chi2_contingency

# 假设我们有一个2x2的列联表，表示男性和女性喜欢猫和狗的人数
observed = [[10, 20],  # 男性喜欢猫和狗的人数
            [15, 30]]  # 女性喜欢猫和狗的人数

chi2, p_val, dof, expected = chi2_contingency(observed)

print(f"chi2 statistic: {chi2}")
print(f"p value: {p_val}")
print(f"degrees of freedom: {dof}")
print(f"expected frequencies: {expected}")

在这个例子中，observed是我们观察到的频数，expected是在男性和女性对猫和狗的喜好完全独立的情况下，我们期望的频数。chi2是卡方统计量，dof是自由度，p_val是P值。

如果P值小于我们事先设定的显著水平（通常为0.05），那么我们就拒绝原假设（男性和女性对猫和狗的喜好独立），认为性别和对猫和狗的喜好之间存在关联。

F检验（F-test）是统计学中一种常用的参数检验方法，主要用于比较两组或多组数据的方差是否相等，或者比较多个模型的拟合优度。

F检验主要有两种常见的应用：

• 方差齐性检验：用于检验两组或多组样本的方差是否相等。这在很多统计分析中是重要的前提假设，比如在进行t检验和方差分析（ANOVA）时，我们通常需要假设各组样本的方差相等。
• 回归分析中的F检验：在多元线性回归分析中，F检验常用于检验模型中所有的自变量是否同时等于0，也就是检验模型的整体显著性。此外，F检验还可以用于比较两个模型的拟合优度，看看增加额外的预测变量是否能显著提高模型的预测准确度。

在进行F检验时，首先要计算F统计量，然后根据F统计量的值和自由度去查F分布表，得到对应的P值。如果P值小于事先设定的显著性水平（通常为0.05），那么我们就拒绝原假设，认为各组样本的方差不等，或者模型的整体显著性达到了统计显著水平。

值得注意的是，F检验的适用条件包括各组样本都应服从正态分布，且样本是随机、独立抽取的。

在Python中，我们可以使用scipy.stats库的f_oneway方法来进行F检验（或者说ANOVA），以判断三个或者更多的样本组是否有显著的差异。下面是一个示例：

from scipy.stats import f_oneway

# 假设我们有三组体重数据，我们想要检验这三组数据的均值是否有显著差异
group1 = [20.1, 20.2, 21.1, 21.4, 21.3, 22]
group2 = [22.3, 22.6, 23.4, 22.8, 22.5, 23.6]
group3 = [21.7, 21.5, 21.2, 22.1, 22.3, 22.7]

F_statistic, p_value = f_oneway(group1, group2, group3)

print('F statistic:', F_statistic)
print('p value:', p_value)

在这个例子中，F_statistic是F统计量，p_value是P值。

如果P值小于我们事先设定的显著水平（通常为0.05），那么我们就拒绝原假设（三组数据的均值相等），认为至少有一组的均值与其他组不同。

需要注意的是，F检验只能告诉我们至少有一组数据的均值与其他组不同，但不能告诉我们哪一组（或哪几组）与其他组不同。如果F检验的结果显著，我们可能还需要进行进一步的多重比较（multiple comparisons）或者事后检验（post-hoc tests）来确定哪些组之间存在显著差异。

ANOVA

ANOVA（Analysis of Variance，方差分析）是一种统计分析方法，用于检验三个或者更多组的均值是否存在显著差异。它扩展了t检验对比两组均值差异的功能，并允许同时比较多组的均值。

主要有以下几种类型的ANOVA：

• 单因素ANOVA（One-way ANOVA）：一个自变量，多个水平。例如，比较不同品牌的汽车的燃油效率。
• 双因素ANOVA（Two-way ANOVA）：两个自变量，可以检验这两个因素对结果的影响，以及他们之间可能存在的交互效应。例如，比较不同品牌和不同型号的汽车的燃油效率。
• 重复测量ANOVA（Repeated Measures ANOVA）：用于处理重复测量数据，即同一对象在不同条件下的测量结果。例如，比较一个人在不同时间段的心率。

F检验是ANOVA中最核心的部分。在进行ANOVA时，首先要计算F统计量，然后根据F统计量的值和自由度去查F分布表，得到对应的P值。如果P值小于事先设定的显著性水平（通常为0.05），那么我们就拒绝原假设，认为各组之间至少有一组的均值与其他组存在显著差异。

需要注意的是，ANOVA假设数据满足正态分布，各组方差相等以及样本独立等条件，如果这些假设不满足，可能需要使用其它非参数方法或者对数据进行适当的转换后再进行分析。

在Python中，可以使用scipy库中的f_oneway函数进行方差分析（ANOVA）。其基础语法如下：

from scipy.stats import f_oneway

data1 = [1, 2, 3, 4, 5]
data2 = [2, 3, 4, 5, 6]
data3 = [3, 4, 5, 6, 7]

F, p = f_oneway(data1, data2, data3)
print('F statistic:', F)
print('p value:', p)

在这个例子中，我们在三个不同的数据组（data1、data2、data3）之间进行了ANOVA测试。如果p值小于预设的显著性水平（例如，0.05），我们将拒绝原假设，即所有组的均值相同，认为至少有一个组的均值与其他不同。

然而，这并不能告诉我们哪些组之间存在显著差异。为了确定这一点，我们需要进行事后测试，也就是多重比较。在Python中，可以使用statsmodels库中的pairwise_tukeyhsd函数进行Tukey HSD测试。例如：

from statsmodels.stats.multicomp import pairwise_tukeyhsd
import numpy as np

# 合并所有数据组
data_all = np.concatenate([data1, data2, data3])

# 创建数据组标签
groups = ['group1']*len(data1) + ['group2']*len(data2) + ['group3']*len(data3)

# 执行Tukey HSD测试
tukey_result = pairwise_tukeyhsd(data_all, groups)
print(tukey_result)

这将为每一对数据组提供一个多重比较的结果，告诉我们哪些组之间存在显著差异。

Z检验是一种统计假设检验，它假设数据遵循正态分布。Z检验通常用于确定观察到的数据偏离预期或理论值的程度是否显著，或者两个数据集的均值是否显著不同。

Z检验计算的是Z分数，这个分数表示的是观察值与平均值之间的标准偏差数。公式如下：

Z = (X – μ) / σ

其中，X是样本均值，μ是总体均值，σ是总体标准差。

Z检验通常用于大样本（样本数大于30）的情况，因为根据中心极限定理，当样本量足够大时，样本均值的分布接近于正态分布。

在Python中，我们可以使用scipy.stats库的zscore函数来计算Z分数。以下是一个例子：

from scipy import stats
import numpy as np

data = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
z_scores = stats.zscore(data)
print(z_scores)

这段代码将为数据集中的每个值生成一个Z分数，这个分数表示该值与平均值的距离（以标准差为单位）。

如果你要进行Z检验，可以使用statsmodels库中的ztest函数。以下是一个例子：

from statsmodels.stats.weightstats import ztest

data1 = [1.1, 1.2, 1.3, 1.4, 1.5]
data2 = [1.6, 1.7, 1.8, 1.9, 2.0]
z_statistic, p_value = ztest(data1, data2)
print(f'Z statistic: {z_statistic}, p-value: {p_value}')

这段代码将比较data1和data2两个数据集的均值是否显著不同。如果p值小于预定的显著性水平（通常为0.05），我们就拒绝原假设（即两个样本的均值相等）。

A/B测试中的假设检验

A/B测试是一种用于比较两种（或更多）版本的产品或页面，看哪种的效果更好的实验方式。在A/B测试中，我们可能会比较两种不同的用户界面设计，看哪一种能带来更高的用户参与度或转化率等。

这里的假设检验就派上用场了。在做A/B测试的时候，我们往往都会有一个零假设（null hypothesis）和一个备择假设（alternative hypothesis）。在A/B测试中，零假设通常是“新的版本和原有的版本在效果上没有差别”。而备择假设则是“新的版本在效果上优于（或不如）原有的版本”。然后我们就可以利用统计学知识，例如t检验，Z检验等，根据收集到的数据来判断我们是否应该拒绝零假设。

假设我们进行了t检验，得到了一个p值。如果这个p值小于我们预定的显著性水平alpha（通常取0.05），那么我们就有足够的证据拒绝零假设，认为新的APP版本在统计上显著优于（或不如）原有的版本。反之，如果p值大于alpha，那么我们就没有足够的证据拒绝零假设，不能认为新的APP版本在效果上有显著差异。

当然，以上的所有步骤都需要在严格控制实验条件和随机化的基础上进行，才能保证结果的有效性和可信度。例如，我们需要保证测试的两组用户在其他所有特性上都是相同的，只有APP版本不同。

在A/B测试中，常用的假设检验方法有：

• t检验（t-test）：当我们有一个较小的样本（一般小于30）并且数据呈正态分布时，我们可以使用t检验。t检验用于比较两个样本的均值是否有显著差异。
• Z检验（Z-test）：当我们有一个较大的样本（一般大于30）并且数据近似正态分布时，我们可以使用Z检验。Z检验也是用于比较两个样本的均值是否有显著差异。
• 卡方检验（Chi-square test）：当我们的数据是分类的（比如点击与未点击，购买与未购买等），我们可以使用卡方检验。卡方检验用于确定两个分类变量之间是否独立。
• F检验（F-test）：在A/B测试中，当我们需要比较两组或多组数据的方差是否相等时，可以使用F检验。
• ANOVA（Analysis of Variance）：当我们需要比较三个或更多组的均值是否相等时，可以使用ANOVA。

具体使用哪种检验方法，取决于我们的数据类型、分布和我们想要回答的问题。在进行检验之前，我们需要确定适当的零假设和备择假设。

假设检验的陷阱有哪些？

• P值误解：P值是在零假设（通常是我们想要反驳的假设）为真时，得到我们观察到的数据或更极端数据的概率。P值并不是我们支持零假设的证据的度量，也不是零假设为真的概率。很多人错误地认为P值小就意味着零假设大概率为假。
• 对于小样本容量的忽视：在小样本情况下，即使有显著的P值，也可能由于样本量太小而造成误导。大量样本可能会使得一些实际上并不显著的差异也显示为统计上的显著。
• 多重比较的问题：如果进行多次假设检验，那么错误拒绝零假设（即发生第一类错误）的概率就会增加。
• 数据挖掘：如果在数据中反复寻找模式，直到找到一个显著的结果，那么这个结果可能是误导的，因为它可能是随机波动的结果。
• 忽视效应大小：假设检验只能告诉我们观察到的效果是否可能是偶然产生的，但不能告诉我们这个效果的大小。一个小的P值并不一定意味着这个效果在实际中也是重要的。
• 执着于统计显著性：过于看重是否达到统计显著性，可能导致忽视了实际意义和效果。此外，统计显著性并不等同于科学显著性。
• 选择性报告：只报告显著结果，不报告不显著结果，可能导致偏见和误导。
• 误解置信区间：置信区间提供了参数的一个可能的范围，但这并不意味着参数有95%的概率落在置信区间内。
• 零假设的误设：在某些情况下，零假设可能并不是我们真正感兴趣的假设，或者零假设可能不太可能为真。
• 忽视统计功效：对于一个给定的效应大小，样本大小和显著性水平，统计功效是正确拒绝零假设（即发现一个真正存在的效应）的概率。如果统计功效过低，那么我们可能会错过一个真正存在的效应。