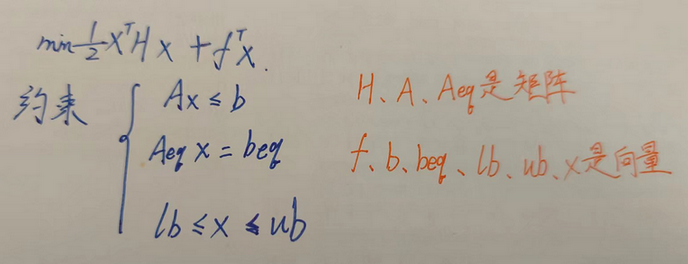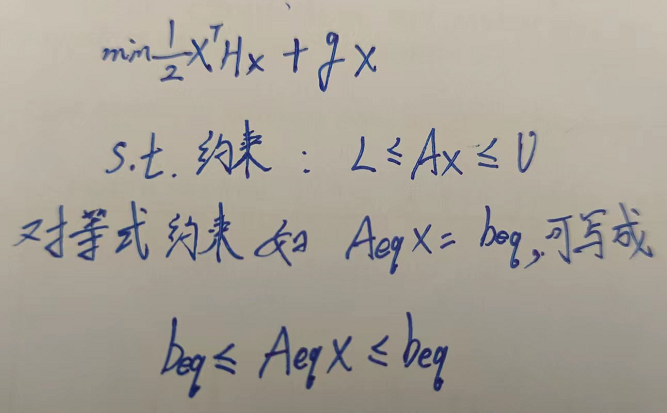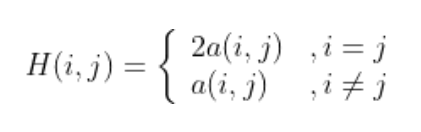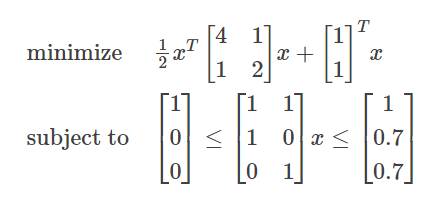二次型问题的求解 C++和Matlab

二次型问题的求解 C++和Matlab

二次规划的一般形式可以表示如下，这也是Matlab中的表示形式

其中x为n维的输入变量，H为n×n维的对称矩阵，f为n维向量。 A是m×n维向量，b是m维向量。二次规划的要求就是在该限制条件(约束)下找到一个n维的向量X，使得f(X)的值最小。

另一种形式如下，似乎是OsqpEigen所用的形式

• 如果H是半正定矩阵，那么f(X)是一个凸函数。

• 如果H是正定矩阵，那么全局最小值就是唯一的。

• 如果H=0，那么f(x)只剩线性部分，二次规划问题就变成线性规划问题。

• 如果至少有一个向量x满足约束而且f(x)在可行域有下届，二次规划问题就有一个全局最小值X。

对于维数较低情况，把二次型表达式转为矩阵形式比较简单，矩阵H的元素是二次型中的矩阵元素大小的两倍。 设矩阵H第i行第j列的元素大小为H(i,j)，二次项 xixjxixj 的系数为a(i,j)，则

也就是平方项的系数对应矩阵H的对角元素，可以直接写出。

如果表达式太复杂，无法直接手写，使用Matlab求海森矩阵获得

syms x1 x2;
f = 0.5*x1.^2+x2.^2-x1*x2;
H = hessian(f, [x1, x2]);
% 转换为double类型
H = double(H);
% 输出矩阵
disp(h) 

C++的求解使用osqp-eigen库

#include "OsqpEigen/OsqpEigen.h"
#include <Eigen/Dense>
#include <iostream>

int main()
{
    // allocate QP problem matrices and vectores
    Eigen::SparseMatrix<double> hessian(2, 2);      //P: n*n正定矩阵,必须为稀疏矩阵SparseMatrix
    Eigen::VectorXd gradient(2);                    //Q: n*1向量
    Eigen::SparseMatrix<double> linearMatrix(2, 2); //A: m*n矩阵,必须为稀疏矩阵SparseMatrix
    Eigen::VectorXd lowerBound(2);                  //L: m*1下限向量
    Eigen::VectorXd upperBound(2);                  //U: m*1上限向量
    // 注意稀疏矩阵的初始化方式,无法使用<<初始化
    hessian.insert(0, 0) = 2.0; 
    hessian.insert(1, 1) = 2.0;
    std::cout << "hessian:" << std::endl << hessian << std::endl;
    gradient << -2, -2;
    // 注意稀疏矩阵的初始化方式,无法使用<<初始化
    linearMatrix.insert(0, 0) = 1.0; 
    linearMatrix.insert(1, 1) = 1.0;
    std::cout << "linearMatrix:" << std::endl << linearMatrix << std::endl;
    lowerBound << 1, 1;
    upperBound << 1.5, 1.5;
    // instantiate the solver
    OsqpEigen::Solver solver;
    // settings
    solver.settings()->setVerbosity(false);
    solver.settings()->setWarmStart(true);
    // set the initial data of the QP solver
    // NumberOfVariables 与 NumberOfConstraints 跟 Hessian 矩阵的维数对应上
    solver.data()->setNumberOfVariables(2);   //变量数n
    solver.data()->setNumberOfConstraints(2); //约束数m
    if (!solver.data()->setHessianMatrix(hessian) || )
        return 1;
    if (!solver.data()->setGradient(gradient))
        return 2;
    if (!solver.data()->setLinearConstraintsMatrix(linearMatrix))
        return 3;
    if (!solver.data()->setLowerBound(lowerBound))
        return 4;
    if (!solver.data()->setUpperBound(upperBound))
        return 5;
    // instantiate the solver
    if (!solver.initSolver())
        return 6;

Eigen::VectorXd QPSolution;
    // solve the QP problem
    if (!solver.solve())
    {
        return 7;
    }
    QPSolution = solver.getSolution();
    std::cout << "QPSolution" << std::endl
              << QPSolution << std::endl; //输出为m*1的向量
    return 0;
}

结果为 1.0003, 1.0003

Matlab

x = quadprog(H,f,A,b,Aeq,beq,lb,ub) 在满足 lb ≤ x ≤ ub 的限制条件下求解上述问题。输入 lb 和 ub 是由双精度值组成的向量，这些限制适用于每个 x 分量。如果不存在等式约束，请设置 Aeq = [] 和 beq = []

H = [2 0; 0 2];
g = [-2; -2]

A = [1 0; 0 1];
b = [1.5; 1.5];
lb = [1; 1];

[x,fval,exitflag,output,lambda] = quadprog(H,g,A,b,[],[],lb);

结果直接为 1.0000, 1.0000. 比osqp-eigen更精确。

x是解。 fval是解处的目标函数值

python

OSQP的python的使用很简单，如果只是求解OSQP，不用C++，可以优先用python。 安装步骤

import osqp
import numpy as np
from scipy import sparse

# Define problem data
P = sparse.csc_matrix([[4, 1], [1, 2]])
q = np.array([1, 1])
A = sparse.csc_matrix([[1, 1], [1, 0], [0, 1]])
l = np.array([1, 0, 0])
u = np.array([1, 0.7, 0.7])
# Create an OSQP object
prob = osqp.OSQP()
# Setup workspace and change alpha parameter
prob.setup(P, q, A, l, u, alpha=1.0)
# Solve problem
res = prob.solve()

参考:
Matlab中的quadprog函数
OSQP库计算标准二次规划
Matlab计算二次规划