Dynamic Programming: Prologue

Hello. This is a prologue to my previous posts, in which I'm going to briefly introduce a reader into the terminology of dynamic programming. This is not an exhaustive guide, but merely a preamble, so that an unprepared reader can get a full picture the same way I see it.

Basic Terms

Dynamic programming – the way to solve a problem by parametrizing it in such a way that an answer for some values of the parameters would help us find the answer for the other values of the parameters; and then finding the answer for all possible parameters' values.

DP state – a specific set of values for each parameter (a specific subtask).

DP value – the answer for a specific state (subtask).

Transition from state A to state B – a mark meaning that in order to know the value for the state B, we need to know the answer for the state A.

Implementing a transition from A to B – some action done when the answer for the state A is already known, satisfying the condition: if you implement every transition into the state B then we will know the answer for the state B. The very action can vary from problem to problem.

Basic DP state – a state, which has no transitions into it. The answer for such a state is found directly.

DP graph – a graph where every vertex corresponds to a state and every edge corresponds to a transition.

Computation

To solve a problem we need to make a DP graph – to determine which transitions there are and how to implement them. Of course, DP graph must not content any cycles. Then we have to find the answer for every basic state and start implementing the transitions.

We can implement the transitions in any order as long as this rule holds true: do not implement a transition from state A before a transition into state A. But most often people use two ways to do it: transitions back and transitions forward.

Transitions back implementation – go through all the vertices in the order of topological sorting and for each fixed vertex implement the transitions into it. In other words, on every step we take an un-computed state and compute the answer for it.

Transitions forward implementation – go through all the vertices in the order of topological sorting and for each fixed vertex implement the transitions from it. In other words, on every step we take a computed state and implement the transitions from it.

In different cases different ways to implement transitions are more suitable, including some "custom" ways.

Example

Unlike previous posts I will not dive into details of how to come up with a solution, but will only demonstrate the introduced terms in action.

AtCoder DP Contest: Задача K Two players take turns to pull stones from a pile, on a single turn one can pull a[0], ..., a[n - 2] or a[n - 1] stones. Initially there are k stones in the pile. Who wins given that they play optimally?

The parameter of the DP will be i – how many stones are initially in the pile.

The value of the DP will be 1 if the first player wins for such a subtask and 0 otherwise. The answers will be stored in the arraydp[i]. The state i = x itself is often denoted as dp[x] for short, I will also use this notation. Let's call a position "winning" if the one who makes the first turn in it wins. A position is a winning one iff there is a move into a losing one, i.e. dp[i] = 1 if dp[i - a[j]] = 0 for somej (0 <= j < n, a[j] <= i), otherwise dp[i] = 0.

Thus, there will be transitions from dp[i - a[j]] into dp[i] for every i and j (a[j] <= i <= k, 0 <= j < n).

The implementation of a transition from A to B in that case is: if dp[A] = 0 set dp[B] = 1. By default every state is considered to be a losing state (dp[i] = 0).

The basic state in that case is dp[0] = 0.

The DP graph in case of k = 5, a = {2, 3}:

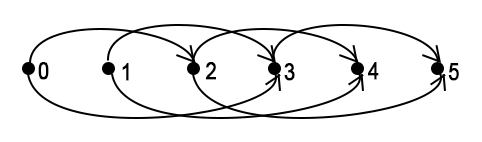
In this code I use the transitions back implementation.

Without any optimizations the time complexity is equal to the number of transitions, in that case it's O(nk).

Another example

AtCoder DP Contest: Задача I There are n coins, i-th coin comes up heads with the probability of p[i]. Find the probability that there will be more heads than tails if you toss every coin one time.

The parameters of the DP will be i – how many of the first coins we consider and j – how many shall come up heads.

The value of the DP will be the probability that exactly j would come up heads if you toss the first i coins, it will be stored in the array dp[i][j]. If i > 0 there are two ways to get j coins come up heads: either among the first i - 1 coins j - 1 come up heads and then the next also comes up heads: this is possible if j > 0, the probability of such event isdp[i - 1][j - 1] * p[i - 1]; or among the first i - 1 coins j come up heads and the next does not come up heads: this is possible if j < i, the probability of such event is dp[i - 1][j] * (1 - p[i - 1]). dp[i][j] will be the sum of these two probabilities.

Thus, there will be transitions from dp[i][j] to dp[i + 1][j + 1] and to dp[i + 1][j] for all i and j (0 <= i < n, 0 <= j <= i).

The implementation of a transition from A to B in this case is: add the answer for the state A times the probability of this transition to the answer for the state B. By default every probability to end up in a state is considered to be 0 (dp[i][j] = 0).

This solution uses the Process Simulation approach, read my post to understand it better.

The basic state in this case is dp[0][0] = 1.

The DP graph in case of n = 3:

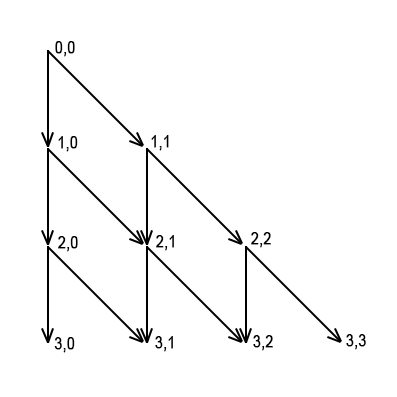
In this code I use the transitions forward implementation.

The number of transitions (and so is the time complexity) in that case is O(n^2).

Conclusion

After reading this article I recommend reading my two previous posts. In there I tell about the two types of dynamic programming and for me this classification seems crucial for further understanding.

Two Kinds of Dynamic Programming: Process Simulation

How to solve DP problems: Regular Approach

If you want to know more, I remind that I do private lessons on competitive programming, the price is $25/h. Contact me on Telegram, Discord: rembocoder#3782, or in CF private messages.