转动布朗运动理论

本人这学期实习关于水分子的转动，所用的理论模型植根于1963年喀山教育学院E. N. Ivanov发表在Soviet Physics JETP上的一篇文章。文章讨论了最简单的情况，对于球谐对称的分子各向同性的转动进行了讨论。本人的工作中需要对这一模型进行延伸，故在这里复述一下，理清思路。

首先说明一下分子转动的基本图像。Debye和Frenkel指出，分子的转动过程如同平动布朗运动一样，在短时间内于平衡位置附近小幅振动，经过足够长时间后发生大幅度转动，平衡位置（或者说平衡指向）随之发生转移。平衡指向的转移幅度与分子的尺度负相关，一般小分子的转动幅度较大（可称为跳跃），而大分子的转移幅度较小，甚至可以接近转动扩散模型。以水为例：（图来自参考文献2）

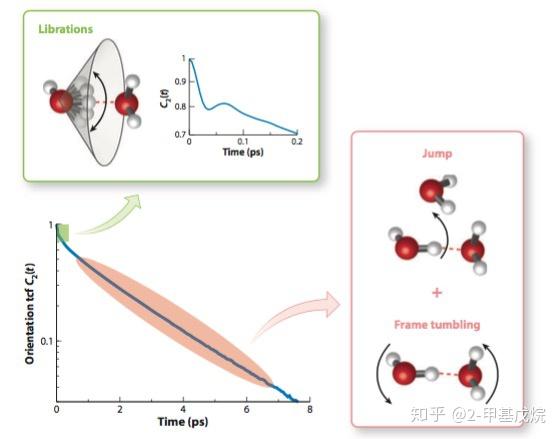
在大约200fs的时间尺度内，水分子的OH键主要在平衡位置附近振动，振幅为一满足高斯分布的随机变量。偶然大尺度的振动会导致原先平衡位置处的氢键断裂，如果此时同时有第三个水分子的氧原子在合适的方向靠近，则容易驱使OH键与之形成新的氢键，平衡指向发生转移，即发生了所谓的跳跃。

我们假设跳跃过程之间是相互独立的，即认为通过跳跃实现的转动时一个马尔可夫过程。考虑 坐标系，其中 为转过的角在转动轴在 方向的投影上的分量。那么转过的角 自然是 的函数。设转动操作为 ，则 。

考虑 次跳跃后分子的指向 。我们定义 次跳跃后分子指向为 的概率密度为 。考虑到跳跃过程的马尔可夫性，我们有：

其中 为分子在 次跳跃后的指向， 为从 到 的跳跃角。可见 和 两者并不独立，这并不是一个二重积分。实际上，这只是一个一重积分，我们需要写出旋转操作除去多余变量。这里积分是对跳跃角 进行的，因而我们设法将 相关的以 表示：

代入上式有

由于 ()张成SO(3)群的不可约表示空间，对 的求解可以通过将其用Wigner D矩阵展开实现：

其中

原则上，求解过程即是对系数 的求解。将展开的 代回关于它的原方程，我们可以得到以下递推关系：

注意到 部分其实是对 转动操作的期望，即Wigner D矩阵 的均值，我们记为 ，则系数矩阵的递推关系可以用矩阵表为：

其中上标 为矩阵转置。由于矩阵 与 无关，类比等比数列，我们有通项公式： 。于是接下来的任务便是根据初始条件得到初始系数矩阵 。我们给定初始时刻分子指向为 ，则初始时刻分子指向概率密度为

考虑到D矩阵的归一化条件：

我们用D矩阵表出0时刻系数矩阵： （两边同乘以欲求系数矩阵元对应位置的另一矩阵元的共轭后同时对 积分即可。）

代回通项公式，我们得到: 。由此我们可以得到 通过展开得到的解： 。由于 ，我们可以把上述方程简写为：

由此我们表出了单分子转动随机行走问题的解。对于各向同性的转动，给定跳跃角，跳跃沿任意方向的概率相同，即 在三维转动操作下守恒。这就要求转动操作的期望矩阵在任意三维转动操作下不变，即 。由于D矩阵群是SO(3)群的不可约表示，由Schur引理， ， 为SO(3)代数的Casimir算符本征值为 的不可约表示空间上的单位算符的矩阵。于是将 代回原解，我们有

，其中 。

以上讨论的是 次跳跃后分子指向为 的概率密度，所谓的时间只是指跳跃次数。真实的问题中，我们是在连续的一段时间内进行观测。因而，我们更关心给定初始指向 ，一段时间 后分子的指向概率密度分布 。在这段时间内，发生的是若干次跳跃，因而我们可以在 和 这两个概率密度值之间建立联系。显然我们可以认为分子指向的跳跃，即平衡指向的跳跃，是一个泊松过程。对于泊松过程，给定一段时间 ，期间发生 次跳跃的概率为 其中 为两次相邻跳跃间的平均时间间隔。由于我们关心大量分子长时间的平均运动情况，我们可以认为 是在时间 上 的期望：

代入 和 ，我们得到

这里我们便解出了 。其中体现具体过程条件，如扩散近似等，的便是单次跳跃期望矩阵 ，其中 的性质体现了过程的某些性质，比如是否各向同性，具有哪些对称性等。代入具体的 就得到具体过程的解。对于各向同性的转动，前面说过 ，因而我们有 其中 。

参考文献：

1. E. N. Ivanov, Theory of Rotational Brownian Motion, JETP, 1963
2. D. Laage et al. Annu. Rev. of Phys. Chem., 2011