计算机图形学基础（3）——观测变换

前面上一篇文章我们介绍了计算机图形学中的数学基础，包括：2D 变换、3D 变换、齐次坐标等。本文，我们则来介绍将三维模型投影到二维屏幕的数学原理。

我们将三维模型投影到二维屏幕的过程称之为 观测变换（Viewing Transformation）。

事实上，观测变换和我们平时拍照一样，总体可以分成三个步骤：

• 摆放物体。在图形学中称为 模型变换（Model Transformation）
• 摆放相机。在图形学中称为 视图变换（View Transformation）
• 拍照。在图形学中称为 投影变换（Project Transformation）

根据这三个步骤的英文缩写，观测变换也可以称为 MVP 变换。不过在图形学中，并不是严格按照这个顺序来执行的，而是先进行视图变换，再进行模型变换。至于为什么，我们稍后再解释。

下面，我们来分别介绍这三种变换。

视图变换也称为相机变换（Camera Transformation），视图的内容本质上是由相机的位置决定的，因此这里我们真正要做的是相机变换。

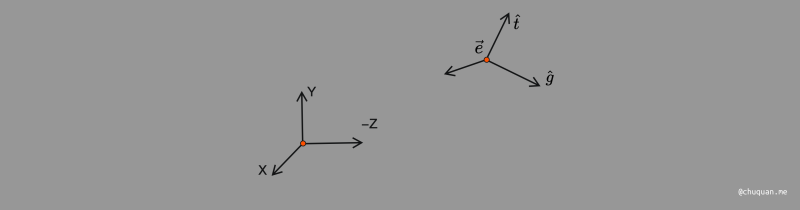
首先，我们使用如下三个向量来描述相机的 原始位置，从而唯一确定其位置、观测方向、画面方向。

• 位置：e→
• 观测方向：g^
• 向上方向：t^

为了方便后续的计算，我们将相机放置到空间坐标系的原点，具体如下：

• 位置：原点坐标
• 观测方向：-Z
• 向上方向：Y

这里我们将变换后的观测方向设置为 -Z，而在有些渲染引擎中观测方向为 Z。这主要取决于空间坐标系的定义，本文我们使用的是右手坐标系。

如何变换？

那么具体我们该如何进行变换呢？一种非常直观的方法，按照四个步骤进行变换：

• 将 e→ 平移变换至原点
• 将 g^ 旋转变换至 -Z
• 将 t^ 旋转变换至 Y
• 将 g^×t^ 旋转变换至 X

很显然，变换矩阵为平移变换和旋转变换的组合，即 Mview=RviewTview。其中，我们很容易就能求解平移变换的变换矩阵，如下。

Tview=(100−xe010−ye001−ze0001)

这里的难点在于求解几个旋转变换的变换矩阵 Rview。那么，该如何求解呢？这里我们转换一下思路，考虑将位于原点的目标位置逆向转换至原始位置。通过这种方式我们可以得到 Rview 的逆矩阵 Rview−1。具体求解过程如下所示。

解得：(???0???0???00001)(1000)=(xg^×t^yg^×t^zg^×t^0)(???0???0???00001)(0100)=(xtytzt0)(???0???0???00001)(0010)=(x−gy−gz−g0)解得：Rview−1=(xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001)

由于旋转矩阵是正交矩阵，所以旋转矩阵的逆矩阵就是它的转置矩阵。由此得到：

Rview=(xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001)

根据相对性原理，相机完成了特定的变换后，我们也需要对模型进行同样的变换，这样通过相机投影得到的画面才会相对不变。

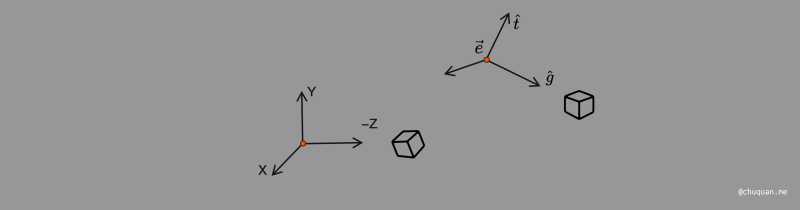
根据上述的相机变换，我们得到了对应的变换矩阵。根据此变换矩阵，我们再对空间中的所有模型进行变换，即完成了模型变换。之后，我们即可进行投影变换。

由模型和相机要进行相同的变换，因此也将模型变换和视图变换统称为 模型视图变换（ModelView Transformation）。

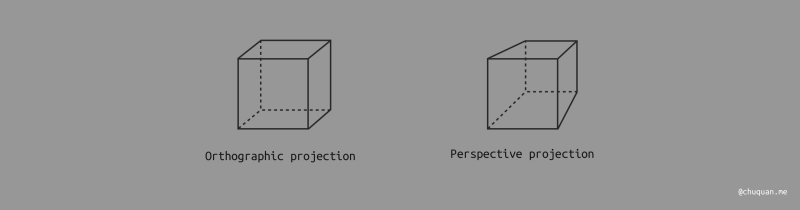
投影变换本质上就是将 3D 模型投影到 2D 画布的过程，具体可以分为两种：

• 正交投影（Orthographic Projection）：一般用于工程制图软件，不具有近大远小的透视效果。
• 透视投影（Perspective Projection）：一般用于游戏引擎、渲染引擎，模拟真实的效果。

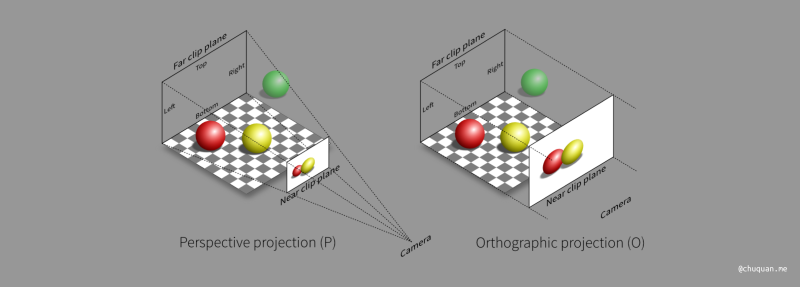
事实上，正交投影可以认为是一种特殊的透视投影，即相机位于无限远的位置，如下所示。

下面，我们先来介绍一下正交投影的两种方法。

方法一非常直观，即丢弃 Z 坐标，直接转换成二维坐标系，然后再将其缩放至 [−1,1]2 的矩形区域，如下所示。为什么要缩放至 [−1,1]2 的矩形区域？事实上，这也是为了方便后续计算，是一种约定俗成的做法。当然，这种方式也存在一个问题，无法直接判断模型之间的远近关系，这个我们后续再讨论。

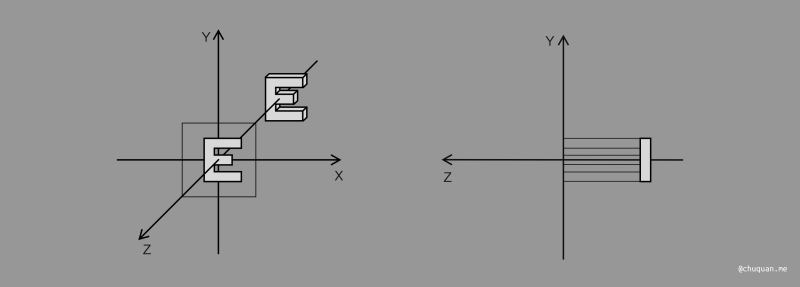
不过，更普遍的做法是方法二，包括后续的透视投影也采用了这种方法。

方法二提出了一个 观测空间（View Volumne）的概念，这一点非常重要。对于正交投影，它的观测空间是一个无限长的长方体，其中以 2D 画布为近面，如下所示。

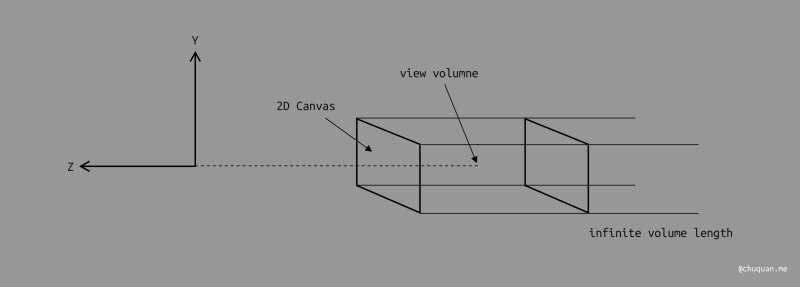
由于 2D 画布可能是任意比例的矩形，为了方便计算，我们将这个长方体的观测空间转换成成一个规范立方体（Canonical Cube），即 [−1,1]3 的空间。

在将观测空间转换成规范立方体的过程中，我们会组合平移、缩放等变换，如下所示。

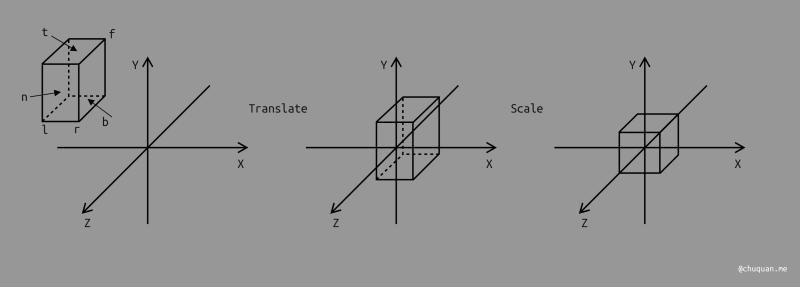
很显然，要将模型转换成标准立方体，我们必须计算出变换矩阵 Mortho。由于投影变换不涉及旋转，因此变换矩阵相对而言比较容易求解，如下所示。

Mortho=SorthoTortho=(2r−l00002t−b00002n−f00001)(100−r+l2010−t+b2001−n+f20001)

在将观测空间转换成规范立方体的过程中，我们计算得到了变换矩阵 Mortho。根据相对不变性原理，我们要使用 Mortho 对空间中所有物体进行同样的变换。这个过程，这里我们不再赘述。

透视投影则借鉴了正交投影的做法，只不过相对而言，它多了一步压缩过程，也就是说，透视投影 = 压缩 + 正交投影。

下面，我们重点介绍一下压缩。

透视投影不同于正交投影，它的观测空间是一个无限长的纺锤体，其中以 2D 画布为近面，如下所示。

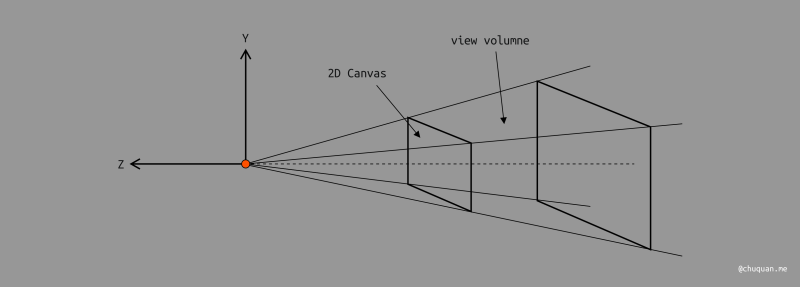
压缩的本质就是将透视投影的观测空间压缩成正交投影的观测空间，即将纺锥体转换成长方体。然后，透视投影就换转化成了正交投影了。

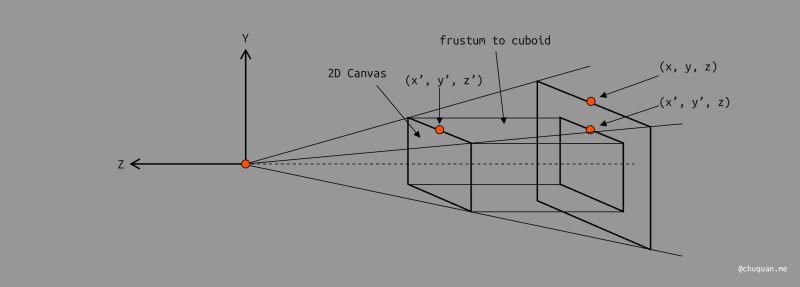
那么，我们该如何求解压缩变换的变换矩阵 Mpersp−>ortho 呢？

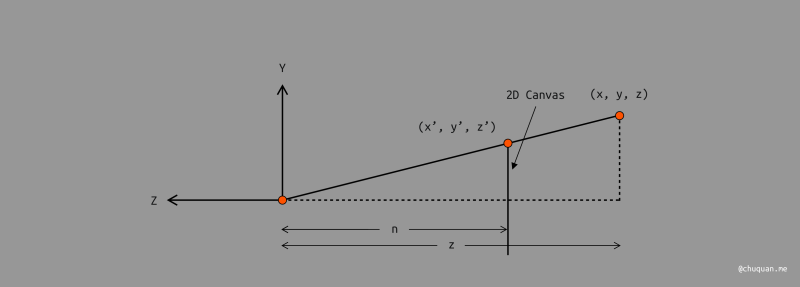
首先，由相似三角形定理，如上图所示，我们可以得出：

y′=nzy;x′=nzx

然后，我们基于齐次坐标，结合三角形定理，计算得出投影点的坐标：

(x′y′z′1)=(nx/zny/z?1)=(nxny?z)

接下来，我们准备求解变换矩阵 Mpersp−>ortho4×4，得出一下关系式：

解得：Mpersp−>ortho(xyz1)=(nxny?z)解得：Mpersp−>ortho=(n0000n00????0010)

最后，我们来求解第三行的值。我们基于两个以下两个依据：

• 近平面上的点的值不会变化，即 2D 画布上的值不变。
• 远平面上的在 Z 轴上的点不会变化。

根据第一个依据，我们可以得出以下关系式。即将 z 替换成 n。

推导：解得：Mpersp−>ortho(xyz1)=Mpersp−>ortho(xyn1)=(xyn1)=(nxnyn2n)推导：(????)(xyn1)=n2解得：(????)=(00??)

我们使用 (0, 0, A, B) 抽象表示 (0, 0, ?, ?)。根据两条依据，我们可以得到一个二元一次方程组，如下所示。

解得：(00AB)(xyn1)=n2=>An+B=n2(00AB)(00f1)=(00f2f)=>Af+B=f2解得：A=n+fB=−nf

综上述，求解得出压缩变换的变换矩阵如下所示，其中 f 是一个动态值，即空间点 (x, y, z) 的 z 值。

Mpersp−>ortho=(n0000n0000n+f−nf0010)

对于透视投影，我们首先求解观测空间的压缩变换的变换矩阵 Mpersp−>ortho，然后再利用在将转换后的长方体观测空间转换成规范立方体，即上文正交投影中求解的 Mortho。

当然，根据相对不变性原理，我们还要将这两个变换矩阵应用到空间中所有的物体上，对它们进行变换。

当 MVP 变换完成之后，我们则要开始将投影内容绘制到 2D 画布中，其中包含了裁剪和视口变换两个步骤。

无论是正交投影还是透视投影，我们都将观测空间转换成了一个规范立方体，同时将转换矩阵应用到空间中的所有物体中。

之后，我们就可以通过规范立方体对空间进行裁剪，只保留规范立方体内的物体，如下所示。很显然，只有在规范立方体中的部分才是我们可以看见的部分。

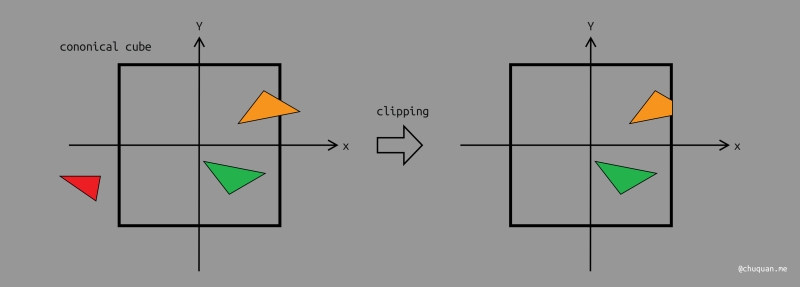
视口（Viewport）本质上就是我们所说的 2D 画布，即屏幕。我们知道屏幕有各种各样的分辨率，宽高比。为了处理这种情况，我们将 2D 画布抽象成一个 [−1,1]2 的规范平面。然后通过视口变换将它映射到真正的视口中。

假设真实视口的宽度是 width，高度是 height，那么视口变换就是将 [−1,1]2 的平面转换成 [0,width]×[0,height] 的平面。

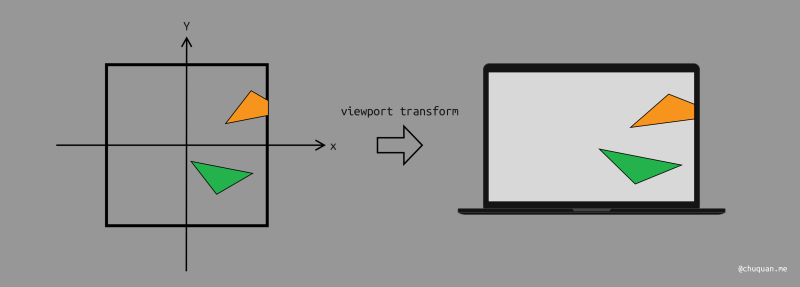
对此，我们很容易求解变换矩阵，如下所示。

Mviewport=(width200width20height20height200100000)

本文，我们主要介绍了观测变换的几个重点内容，包括视图变换、投影变换。其中，我们重点介绍了投影变换中的两种：正交投影和透视投影。

投影变换中提到了一个重要概念——观测空间。我们会将观测空间转换成一个规范立方体，根据相对不变性原理，对空间中所有物体做同样的变换。其中透视投影稍有复杂一点，我们会将纺锤体的观测空间转换成长方体的观测空间。

最后，我们将规范立方体以外的内容进行裁剪，并采用视口变换将内容映射到具体的屏幕上。

后面，我们将基于本章的内容继续介绍计算机图形学的相关基础。

1. 《GAMES 101》
2. Image Processing and Computer Graphics——Rendering Pipeline, Matthias Teschner.