高中数学学习笔记 – 椭圆

我怎么也沦落到发这种文章了。

整理都整理完了，不发白不发。

给定两点 F1,F2F_1, F_2F1​,F2​，令 ∣F1F2∣=2c|F_1F_2| = 2c∣F1​F2​∣=2c，存在动点 PPP 满足 ∣PF1∣+∣PF2∣=2a(2a>2c)|PF_1| + |PF_2| = 2a(2a>2c)∣PF1​∣+∣PF2​∣=2a(2a>2c)，则 P 的轨迹曲线为椭圆。

2a = 2c 时 P 的轨迹为线段，也就是线段 F1F2F_1F_2F1​F2​；
2a < 2c 时 P 不存在。

• F1,F2F_1, F_2F1​,F2​ 称为焦点。

---

第二定义：

准线：x=±a2cx = \pm \frac{a^2}{c}x=±ca2​

令 PPP 到左准线距离为 d1d_1d1​，到右准线距离 d2d_2d2​。

PF1d1=PF2d2=e(e∈(0,1)) \frac{PF_1}{d_1} = \frac{PF_2}{d_2} = e ( e \in (0,1) )d1​PF1​​=d2​PF2​​=e(e∈(0,1))

2 几何性质

2.1 标准式

焦点在 xxx 轴上：

x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )a2x2​+b2y2​=1(a>b>0)

焦点在 yyy 轴上：

y2a2+x2b2=1(a>b>0)\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1 ( a > b > 0 )a2y2​+b2x2​=1(a>b>0)

2.2 一般式

Ax2+By2=1(A>0,B>0,A≠B) Ax^2 + By^2 = 1 (A>0,B>0,A \neq B)Ax2+By2=1(A>0,B>0,A=B)

• 注意 A≠BA \neq BA=B 不然就是圆了。

2.3 a, b, c 的关系

a2=b2+c2 a^2 = b^2 + c^2 a2=b2+c2

2.4 范围

x∈[−a,a],y∈[b,−b]x \in [-a,a], y \in [b,-b]x∈[−a,a],y∈[b,−b]

• (a2−e2x02)(a^2-e^2x_0^2)(a2−e2x02​)
• 最大值：x0=0x_0 = 0x0​=0 时，取 a2a^2a2；
• 最小值：x0=ax_0 = ax0​=a 时，取 a2−c2=b2a^2-c^2=b^2a2−c2=b2。

2.5 对称性

关于坐标轴，(0,0)(0,0)(0,0) 对称。

2.6 长短轴

• 长轴：2a2a2a
• 短轴：2b2b2b
• 焦距：2c2c2c
• 半焦距：ccc

2.7 离心率

表示椭圆的圆扁。

e=cae=\frac{c}{a}e=ac​

• 显然 e∈(0,1)e \in (0,1)e∈(0,1) 因为 a>ca > ca>c

e→1e \to 1e→1，越扁。e2=c2a2=1–b2a2e^2 = \frac{c^2}{a^2} = 1 – \frac{b^2}{a^2}e2=a2c2​=1–a2b2​

2.7.1 求法

1. e2=c2a2e^2 = \frac{c^2}{a^2}e2=a2c2​
2. 构建 a,ca,ca,c 齐次式
3. 特殊位置特殊值
4. 焦点三角形底角 α,β\alpha, \betaα,β 有 e=sin⁡(α+β)sin⁡α+sin⁡βe = \frac{\sin(\alpha + \beta)}{\sin \alpha + \sin \beta}e=sinα+sinβsin(α+β)​

2.8 通经

过焦点，两端点位于椭圆上，垂直于 xxx 轴的线段。

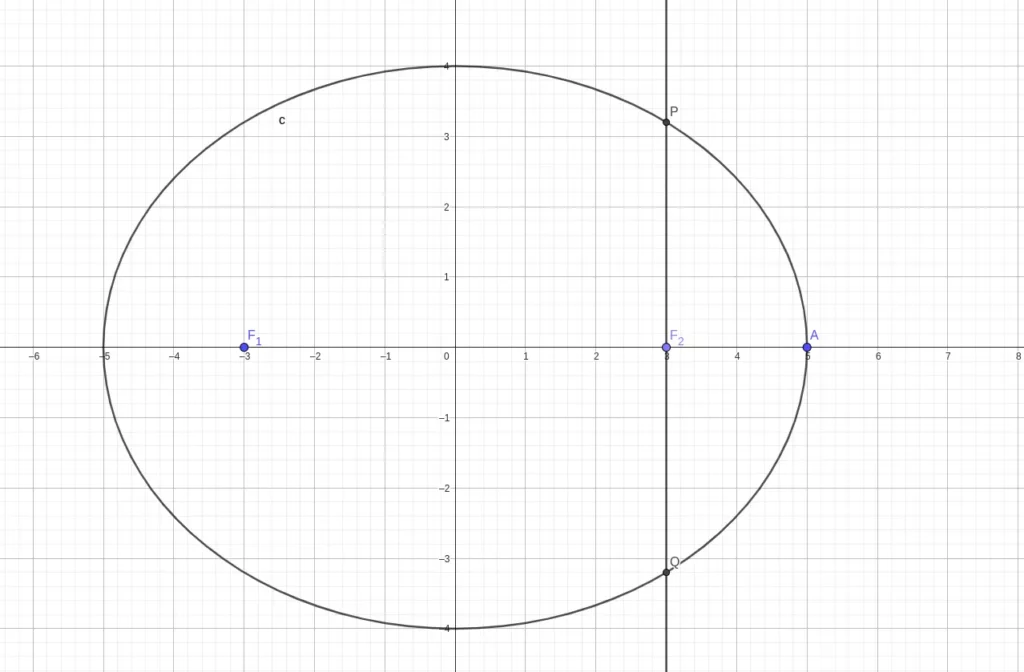
即图中 PQPQPQ。

有 PQ=b2aPQ = \frac{b^2}{a}PQ=ab2​

3.1 焦点三角形

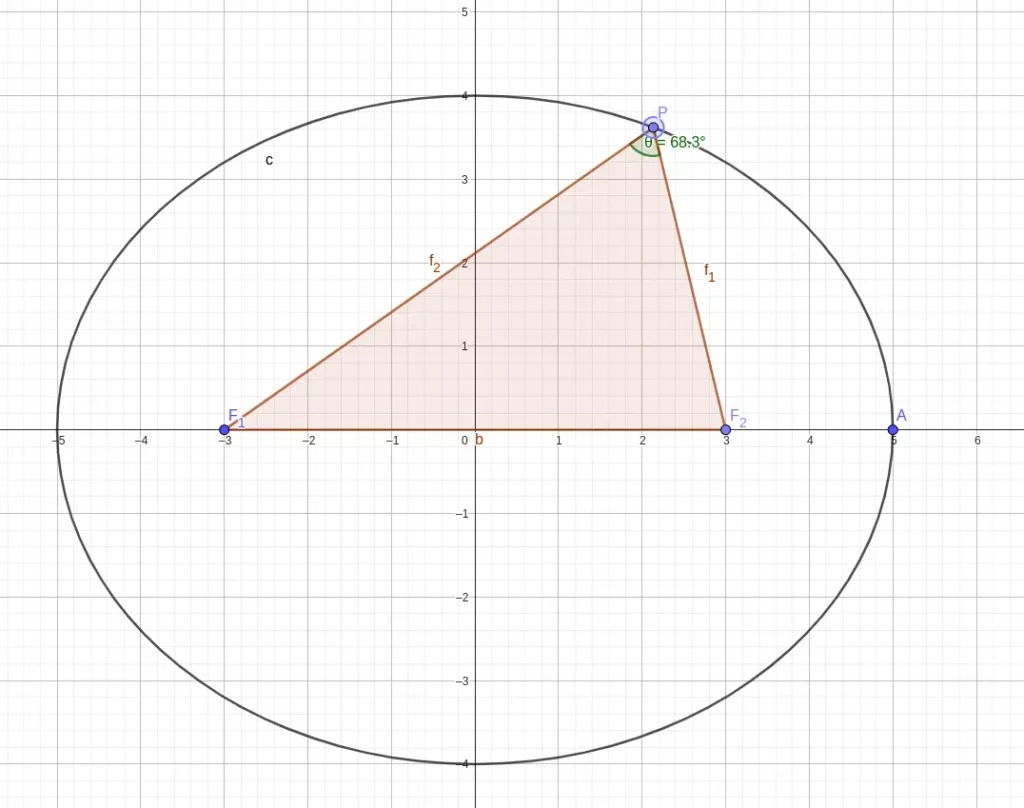
如图，以椭圆上一点 PPP 和焦点 F1F2F_1F_2F1​F2​ 构成的三角形 △PF1F2\triangle PF_1F_2△PF1​F2​ 称为焦点三角形。

• ∣PF1∣+∣PF2∣=2a|PF_1|+|PF_2| = 2a∣PF1​∣+∣PF2​∣=2a
• ∣PF1∣2+∣PF2∣2–2∣PF1∣∣PF2∣cos⁡θ=∣F1F2∣2=2c2|PF_1|^2 + |PF_2|^2 – 2|PF_1||PF_2| \cos \theta = |F_1F_2|^2 = 2c^2∣PF1​∣2+∣PF2​∣2–2∣PF1​∣∣PF2​∣cosθ=∣F1​F2​∣2=2c2
• S△=12∣PF1∣∣PF2∣sin⁡θ=b2tan⁡θS \triangle = \frac{1}{2}|PF_1||PF_2| \sin \theta = b^2 \tan \thetaS△=21​∣PF1​∣∣PF2​∣sinθ=b2tanθ
• 周长： 2(c+a)2(c+a)2(c+a)

3.1 延伸三角形

延伸焦点三角形中的非 F1F2F_1F_2F1​F2​ 一边交于椭圆，为延伸三角形。

• 周长：4a4a4a

3.2 焦半径

就是 PF1,PF2PF_1,PF_2PF1​,PF2​

有 PF1=a+ex0PF_1 = a + ex_0PF1​=a+ex0​ PF2=a–ex0PF_2 = a – ex_0PF2​=a–ex0​

代入第二定义证明。

有 PF∈[a–c,a+c]PF \in [ a – c, a + c ]PF∈[a–c,a+c]。

4.1 共焦点

x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )a2x2​+b2y2​=1(a>b>0)

共焦点的椭圆可设

x2a2−k+y2b2−k=1(a>b>0,b2–k>0)\frac{x^2}{a^2-k} + \frac{y^2}{b^2-k} = 1 ( a > b > 0, b^2 – k > 0 )a2−kx2​+b2−ky2​=1(a>b>0,b2–k>0)

4.2 共离心率

x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ( a > b > 0 )a2x2​+b2y2​=1(a>b>0)

共焦点的椭圆可设

x2a2+y2b2=λ(a>b>0,λ>0)\frac{x^2}{a^2} + \frac{y^2}{b^2} = \lambda ( a > b > 0, \lambda > 0 )a2x2​+b2y2​=λ(a>b>0,λ>0)

5.1 中点弦

若 M(x,y)M(x,y)M(x,y) 为椭圆弦 ABABAB 的中点。

有 kAB⋅kOM=−b2a2k_{AB} \cdot k_{OM} = -\frac{b^2}{a^2}kAB​⋅kOM​=−a2b2​

点差法：
有 A(x1,y1),B(x2,y2)A(x_1,y_1), B(x_2, y_2)A(x1​,y1​),B(x2​,y2​) 在椭圆上，即
{x12a2+y12b2=1x22a2+y22b2=1\begin{cases} \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 \\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1 \end{cases}{a2x12​​+b2y12​​=1a2x22​​+b2y22​​=1​
两式做差有
x12–x22a2+y12–y22b2=0\frac{x_1^2 – x_2^2}{a^2} + \frac{y_1^2 – y_2^2}{b^2} = 0a2x12​–x22​​+b2y12​–y22​​=0
整理可得
y1−y2x1−x2=−b2(x1+x2)a2(y1+y2)\frac{y_1-y_2}{x_1-x_2} = -\frac{b^2(x_1+x_2)}{a^2(y_1+y_2)}x1​−x2​y1​−y2​​=−a2(y1​+y2​)b2(x1​+x2​)​

5.2 弦长公式

y=kx+by = kx + by=kx+b 与椭圆交于 A(x1,y1),B(x2,y2)A(x_1,y_1), B(x_2, y_2)A(x1​,y1​),B(x2​,y2​)

有 ∣AB∣=1+k2∣x1–x2∣=1+k2(x1+x2)2−4x1x2=1+1k2(y1+y2)2−4y1y2|AB| = \sqrt{1+k^2}|x_1 – x_2| = \sqrt{1+k^2}\sqrt{(x_1+x_2)^2-4x_1x_2} = \sqrt{1+\frac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}∣AB∣=1+k2​∣x1​–x2​∣=1+k2​(x1​+x2​)2−4x1​x2​​=1+k21​​(y1​+y2​)2−4y1​y2​​

5.3 切线方程

过椭圆上一点 (x0,y0)(x_0,y_0)(x0​,y0​) 切线方程为 x0xa2+y0yb2=1\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1a2x0​x​+b2y0​y​=1

过椭圆外一点 P(x0,y0)P(x_0,y_0)P(x0​,y0​) 的两条，和椭圆的两个切点 P1,P2P_1,P_2P1​,P2​ 所在直线方程：

x0xa2+y0yb2=1\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1a2x0​x​+b2y0​y​=1