2

AVL树和红黑树的模拟实现

 1 year ago
source link: https://blog.51cto.com/u_15132397/5682409
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

我们要遇到C++里面最难一部分了,也是一些大厂有可能出的面试题,比如说手撕一个红黑树.这个博客的内容可能有点耗脑,我尽量和大家分享的接地气一点.

这种树也叫做平衡二叉树.这个是前面二叉搜索树的变种.我们前面谈过,对于比较有序元素,那么搜索二叉树就有点深了,甚至转换成了单只树,那么这样查找的效率就有点低了.所以我们提出的AVL树.所谓的平衡二叉树就是当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度 .这个就是AVL树的定义,至于如何做到,这里我们先不用关心.

我们先来看一下AVL树的特点,一般情况而言,对于那些比较有序的元素,我们插入元素后通过一系列的手段来降低树的高度,并且最后的树仍旧符合二叉搜索树的特点.

AVL树和红黑树的模拟实现_父节点

AVL树 实现

我们已经知道AVL树是什么了,今天我们就要把他给简单的实现出来.这个过程说实话有点难.我们这里实现KV模型的．不过我们们先来把框架给搭出来.

namespace bit
{
  template<class T,class T>
  class AVLTree
  {

};
}



我们前面把大的框架搭出来了,这里就需要开始搭建树的节点了,我们先暂时看一下,后面完善.这里我们已经搭建出来了,我们为何会加入父节点这个原因我们等到用到的时候再说.



struct AVLTreeNode
{
    AVLTreeNode(const T& data = T())
        : _praent(nullptr)
        , _left(nullptr)
        , _right(nullptr)
        , _data(data)
        {} 

AVLTreeNode<T>* _praent;
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;

T _data;
};



现在我们需要在谈一个问题,我们是如何确保左右节点的差距只有一呢?这里需要借助一个平衡因子,父节点的平衡因子记录左右子树高度的差值.这样我们插入的时候就可以看平衡因子的改变,从而判断是不是要移动树了.这里我们平衡因子记录的是右子树减去左子树.至于如何修改平衡因子的值这就有说道了.



AVL树和红黑树的模拟实现_父节点_02



template<class T>
struct AVLTreeNode
{
    AVLTreeNode(const T& data = T())
        : _praent(nullptr)
        , _left(nullptr)
        , _right(nullptr)
        , _data(data)
        , _bf(0)
    {} 

AVLTreeNode<T>* _praent;
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;

T _data;
    int _bf;

};



现在的的我们大框架已经打好了,我们现在开始重点的工作,这个可是比较烧脑的.我们也是只实现插入操作.



template<class T>
struct AVLTreeNode
{
    AVLTreeNode(const T& data = T())
        : _praent(nullptr)
        , _left(nullptr)
        , _right(nullptr)
        , _data(data)
        , _bf(0)
    {} 

AVLTreeNode<T>* _praent;
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;

T _data;
    int _bf;

};
template<class K, class T>
class AVLTreeV
{
    public:
    typedef AVLTreeNode<T> Node;
    AVLTree()
        :_pRoot(nullptr)
    {}

bool Insert(const T& data)
    {
        return true;
    }
    public:
    Node* _pRoot;
};



首先第一步是简单的搜索二叉树的简单操作.我们先来找到插入的节点在哪里.



bool Insert(const T& data)
{
    // 第一步 判断 第一次 插入
    if (_pRoot == nullptr)
    {
        _pRoot = new Node(data);
        _pRoot->_bf = 0;
        return true;
    }

// 第二步 搜索二叉树 找位置
    Node* cur = _pRoot;
    Node* parent = nullptr;
    while (cur != nullptr)
    {
        if (cur->_data < data)
        {
            // 去 右树 查找
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_data > data)
        {
            // 左树 查找
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            // 我们这里不接受 重复值 ,你可以自己实现
            return false;
        }
    }

// 第三步 new 出来一个节点
    Node* node = new Node(data);
    node->_bf = 0;               // 记住 不要相信构造函数,有可能不是你写的,不会自动默认0
    // 第四步 判断是插入左树还是 右树
    if (parent->_data > data)
    {
        parent->_left = node;
    }
    else
    {
        parent->_right = node;
    }
    // 这里需要链接
    node->_parent = parent;
    cur = node;
    // 更新平衡因子
    // ...
    return true;
}



我们这里预留了最关键的一步,就是更新平衡因子.这里需要讨论的事情是在是太多了.我们首先要判断是插入的节点是左树还是右树,这样方便我们修改父节点的平衡因子.



bool Insert(const T& data)
{
    // 第一步 判断 第一次 插入
    if (_pRoot == nullptr)
    {
        _pRoot = new Node(data);
        _pRoot->_bf = 0;
        return true;
    }

// 第二步 搜索二叉树 找位置
    Node* cur = _pRoot;
    Node* parent = nullptr;
    while (cur != nullptr)
    {
        if (cur->_data < data)
        {
            // 去 右树 查找
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_data > data)
        {
            // 左树 查找
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            // 我们这里不接受 重复值 ,你可以自己实现
            return false;
        }
    }

// 第三步 new 出来一个节点
    Node* node = new Node(data);
    node->_bf = 0;               // 记住 不要相信构造函数,有可能不是你写的,不会自动默认0
    // 第四步 判断是插入左树还是 右树
    if (parent->_data > data)
    {
        parent->_left = node;
    }
    else
    {
        parent->_right = node;
    }
    // 这里需要链接
    node->_parent = parent;
    cur = node;
    // 更新平衡因子
    while (parent != nullptr)
    {
        // 如果 插入的是 右子树
        if (cur == parent->_right)
        {
            parent->_bf++;
        }
        else
        {
            parent->_bf--;
        }

//  开始 检测
        if (parent->_bf == 0)
        {
            break;
        }
        else if (parent->_bf == 1 || parent->_bf == -1)
        {
            cur = parent;
            parent = parent->_parent;
        }
        else if (parent->_bf == 2 || parent->_bf == -2)
        {
            // 这里 才是 大头
            if (cur->_bf == 1 && parent->_bf == 2)
            {
            }
            else if (cur->_bf == -1 && parent->_bf == -2)
            {
            }
            // ...
        }
        else
        {
            assert(false);
        }
    }

return true;
}



前面我们简单的叙述了一下平衡因子的改变,这里具体情况分析一下.首先,我们是按照祖先来更新的,这一点无可置疑



if (cur == prev->_right)
{
    prev->_bf++;
}
else
{
    prev->_bf--;
}



也就说我们修改平衡因子,当我们子树的高度没变,也就是平衡因子为0的时候,停止更新.要是高度变了,变成了1那么肯定是右子树的高度变高了,这就需要我们继续往上面走,要是-1,是左树树高了,也要往上面走.这里最关键的就是-2和2,这个是我们要谈的重点,也是我们需要旋转的条件.



假设右子树比左子树高了两个,而且还满足一定的情况,我们这就使用左单旋.我们先来分析一下情况.



AVL树和红黑树的模拟实现_父节点_03



至于如何旋转我们先暂时不谈,先来说几个具体的情况.



当 h = 0时



AVL树和红黑树的模拟实现_搜索二叉树_04



当 h = 1 时



AVL树和红黑树的模拟实现_父节点_05



当h = 2的时候这里的情况可就多了.



AVL树和红黑树的模拟实现_子树_06



我们就不往后面分析了,这里说一下具体的用法,还是按照理论来进行旋转.



AVL树和红黑树的模拟实现_父节点_07



  • 把subRL给成parent的右子树
  • 把parent 给成subL的左子树
  • 修改逻辑顺序和平衡因子



AVL树和红黑树的模拟实现_父节点_08



if (cur->_bf == 1 && parent->_bf == 2)
{
    // 左旋
    RotateL(parent);
}

void RotateL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;

parent->_right = subRL;
    if(subRL)
        subRL->_praent = parent;
    // 记录 祖父节点
    Node* grandparent = parent->_praent;

parent->_praent = subR;
    subR->_left = parent;

if (grandparent == nullptr)
    {
        // parent 就是 根节点
        _pRoot = subR;
        _pRoot->_praent = nullptr;
    }
    else
    {
        subR->_praent = grandparent;
        // 在判断  原本 的父节点 和 祖父的关系
        if (parent == grandparent->_left)
        {
            grandparent->_left = subL;
        }
        else
        {
            grandparent->_right = subL;
        }
    }

// 修改 平衡因子
    subR->_bf = 0;
    parent->_bf = 0;
}



我们先来把特殊的情况给分析一下,subRL可能为空,也就是h=0,这就造成subRL修改父节点的时候需要判断一下,还有就是你不感觉我们太顺风顺水了吗,你是如何确定parent一定是根节点的,我们前面的模型是一个子树的模型,不一定确保是完整的树.这个问题还是要判断的,否则就会出现问题.



这个就比较简单了,我们这里直接上模型吧.右单旋就是右边高,这里需要向右边移动.



AVL树和红黑树的模拟实现_搜索二叉树_09



AVL树和红黑树的模拟实现_父节点_10



else if (cur->_bf == -1 && parent->_bf == -2)
{
    // 右旋
    RotateR(parent);
    break;
}

void RotateR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    parent->_left = subLR;
    if (subLR)
        subLR->_parent = parent;
    Node* grandparent = parent->_parent;
    parent->_parent = subL;
    subL->_right = parent;

if (grandparent == nullptr)
    {
        _pRoot = subL;
        _pRoot->_parent = nullptr;
    }
    else
    {
        subL->_parent = grandparent;
        if (grandparent->_left == parent)
        {
            grandparent->_left = subL;
        }
        else
        {
            grandparent->_right = subL;
        }
    }
    // 更新平衡因子
    subL->_bf = parent->_bf = 0;
}



我们先来测试一下单旋,也就是我们尽量插入有序的元素,这里就只需要单旋操作.但是这里我们需要注意,这里我们可不是能够确定我们的树是AVL树，只是看看我们代码是不是和逻辑符合．



void test1()
{
    AVLTree<int, int> a;
    for (int i = 0; i < 8; i++)
    {
        a.Insert(i+1);
    }
    cout << "层序遍历" << endl;
    a.levelOrder();
    cout << "中序遍历" << endl;
    a.inorder();
}



AVL树和红黑树的模拟实现_子树_11



现在我们开始一个比较复杂的情况,是双旋的问题.我们要是直接插入8,6,7.这就有意思了.看一下.你会发现简单的单旋是解决不了问题的.这里需要一点手段.



AVL树和红黑树的模拟实现_父节点_12



我们先来看一下模型吧,后面在讨论解决方案.这里就像是一个折线图.



AVL树和红黑树的模拟实现_搜索二叉树_13



这里我们也列举几个具体的情况.



AVL树和红黑树的模拟实现_子树_14



这个时候我们就在想,这个应该如何旋转,这里需要一点变通.我们先来看大方针.



AVL树和红黑树的模拟实现_子树_15



也就是说我们需要以subL做左单旋,后面以parent做右单旋.



else if (cur->_bf == 1 && parent->_bf == -2)
{
    RotateLR(parent);
    break;
}
void RotateLR(Node* parent)
{
    RotateL(parent->_left);
    RotateR(parent);
    // 修改平衡因子
    // ...
}



注意我们旋转是没有问题的,这里可以直接复用前面的,难的是需要修改平衡因子.那么这里面就存在下面的问题,看一看下面的方法



AVL树和红黑树的模拟实现_子树_16



我们需要把这些节点给保存下来,而且还要讨论如何给这些节点修改平衡因子.



void RotateLR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;

RotateL(parent->_left);
    RotateR(parent);
    // 修改平衡因子
    // ...
}



现在我们剩下的问题就是如何修改平衡因子了,我们知道subLR一定是0,但是subL和parent可就不一定了,这需要分情况讨论,那么我们讨论的依据是什么呢?这就有点意思了.我们根据苏subLR的平衡因子的值来讨论.不过我们需要先把它给记录下来,单旋的时候会把它给修改了.我们根据下面的图来修改就可以了.



AVL树和红黑树的模拟实现_子树_17



void RotateLR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    int bf = subLR->_bf;
    RotateL(parent->_left);
    RotateR(parent);
    // 修改平衡因子
    if (bf == 0)
    {
        parent->_bf = 0;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
    else if (bf == 1)
    {
        parent->_bf = 0;
        subL->_bf = -1;
        subLR->_bf = 0;
    }
    else if (bf == -1)
    {
        parent->_bf = 1;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
    else
    {
        assert(false);
    }
}



这个和上面的是一样的,也是折线,我们是需要右单旋加上左单旋.



AVL树和红黑树的模拟实现_搜索二叉树_18



看下解决思路,我这里就不具体的举例子了.



AVL树和红黑树的模拟实现_搜索二叉树_19



else if (cur->_bf == -1 && parent->_bf == 2)
{
    RotateRL(parent);
    break;
}
void RotateRL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    int bf = subRL->_bf;

RotateR(parent->_right);
    RotateL(parent);

// 修改平衡因子

}



我么还是重点关注如何修改平衡因子,这个需要简单的分析一下,但是思路和上面都是一样的.



AVL树和红黑树的模拟实现_子树_20



void RotateRL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    int bf = subRL->_bf;

RotateR(parent->_right);
    RotateL(parent);

// 修改平衡因子
    if (bf == 0)
    {
        subR->_bf = 0;
        parent->_bf = 0;
        subRL->_bf = 0;
    }
    else if(bf == 1)
    {
        subR->_bf = 0;
        parent->_bf = -1;
        subRL->_bf = 0;
    }
    else if (bf == -1)
    {
        subR->_bf = 1;
        parent->_bf = 0;
        subRL->_bf = 0;
    }
    else
    {
        assert(false);
    }

}



我们这里也测试一下乱序的情况,避免代码出现错误.



void test2()
{
    int arr[] = { 1,4,3,7,5,8,1,10 };
    int sz = sizeof(arr) / sizeof(arr[0]);
    AVLTree<int, int> a;
    for (int i = 0; i < sz; i++)
    {
        a.Insert(arr[i]);
    }
    cout << "层序遍历" << endl;
    a.levelOrder();
    cout << "中序遍历" << endl;
    a.inorder();
}



AVL树和红黑树的模拟实现_搜索二叉树_21



AVL树的判定



这里我们需要看看自己写的AVL树到底是不是正确的,这里直接上代码.



public:
    bool isBalanceTree()
    {
        return _IsBalanceTree(_pRoot);
    }
private:
    int _height(Node* root)
    {
        if (root == nullptr)
            return 0;

int lh = _height(root->_left);
        int rh = _height(root->_right);

return lh > rh ? lh + 1 : rh + 1;
    }
    bool _IsBalanceTree(Node* root)
    {
        // 空树也是平衡二叉树
        if (root == nullptr)
            return true;

// 记录 左右节点的高度
        int left = _height(root->_left);
        int right = _height(root->_right);
        int diff = left - right;
        // 判断 平衡因子
        if (abs(diff) >= 2)
        {
            cout << "平衡因子更新错误" << endl;
            return false;
        }
        if (right - left != root->_bf)
        {
            cout << "节点平衡因子不符合实际" << endl;
            return false;
        }
        return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);

}



我们测试一下有序和无序的插入.



void test4()
{
    int N = 1024;
    AVLTree<int, int> a;
    for (int i = 0; i < N; i++)
    {
        a.Insert(i);
    }
    cout << "是否平衡" << a.isBalanceTree() << endl;
}

void test5()
{
    int N = 1024*1024;
    AVLTree<int, int> a;
    srand(time(0));
    for (int i = 0; i < N; i++)
    {
        a.Insert(rand());
    }
    cout << "是否平衡" << a.isBalanceTree() << endl;
}



AVL树和红黑树的模拟实现_子树_22



谈完AVL树,这里我们需要看一下红黑树.你不觉得我们的AVL树太过严格了吗,动不动就是移动子树.我们先来看一下红黑树的定义.



红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的.红黑树的查找效率还是低于AVL树的,但是综合效率是不差的.



我们提取出来两个基本的观点



  • 节点带颜色
  • 通过颜色限制来保证没有一条路劲会大于其他路劲的两倍.



AVL树和红黑树的模拟实现_子树_23



红黑树特性



我们需要分析一下红黑树的特性,为了后面我们实现.



  1. 每个结点不是红色就是黑色
  2. 根节点是黑色的
  3. 如果一个节点是红色的，则它的两个孩子结点是黑色的,也就是红色不连续
  4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点
  5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点) ,弥补特性3



首先我们就要分析一下为何满足上面的特点,这里就可以得到红黑树.首先我们可以这么想,最短的路径假设是黑色,根据特性4,存在相同的黑色节点,那么如果存在最长的节点就是加上一些红色节点,根据特性3,红色节点不能连续,最长的大概就是一红一黑.



红黑树的节点



这里我们需要看看一下红黑树的节点是如何设计的.



enum Colour
{
    RED,
    BLACK
};
template<class K,class V>
struct RBTreeNode
{
    RBTreeNode(const pair<K,V>& kv)
        :_left(nullptr)
        ,_right(nullptr)
        ,_parent(nullptr)
        ,_kv(kv)
        ,_col(RED)
        {}

RBTreeNode<K, V> _left;
    RBTreeNode<K, V> _right;
    RBTreeNode<K, V> _parent;
    pair<K, V> _kv;
    Colour _col;
};



这里我们疑惑为何节点默认是红色?我们可以这想,如果我们是黑色,无论父节点是红色还是黑色都不需要旋转,但是这会造成我插入的元素的一条支路的黑色增加了1,破坏特性4,而且这种情况很难处理.如果默认是红色,如果父节点是红色,根据红色不能连续,需要旋转.但是也只是影响我们父子几个而已.



AVL树和红黑树的模拟实现_子树_24



我们先来把这个数据结构的框架给搭出来.



template<class K, class V>
class RBTree
{
public:
  typedef RBTreeNode<K, V> Node;
private:
  Node* _pRoot = nullptr;
};



这里我们就可以来进行元素的插入了.我们约定当前节点为cur,p为父节点,g为祖父节点,c为叔叔节点,红黑树的插入关键看叔叔,这一点是非常重要的.首先我们前面的插入都是比较简单的,和二叉搜索树一样.



bool Insert(const pair<K, V>& data)
{
    // 第一步 判断 第一次 插入
    if (_pRoot == nullptr)
    {
        _pRoot = new Node(data);
        _pRoot->_col = BLACK;
        return true;
    }

// 第二步 搜索二叉树 找位置
    Node* cur = _pRoot;
    Node* parent = nullptr;
    while (cur != nullptr)
    {
        if (cur->_kv.first < data.first)
        {
            // 去 右树 查找
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > data.first)
        {
            // 左树 查找
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            // 我们这里不接受 重复值 ,你可以自己实现
            return false;
        }
    }

// 知道 节点
    Node* node = new Node(data);
    node->_col = RED;           // 记住 不要相信构造函数,有可能不是你写的,不会自动默认0

// 插入元素
    if (data->first > parent->_kv->first)
    {
        parent->_right = node;
    }
    else
    {
        parent->_left = node;
    }
    node->_parent = parent;
    cur = node;

// ...
}



我们这里就需要判断了,想一下我们节点是红色,如果我的父亲是黑色,这里就可以直接插入,什么都不用做.如果要是父亲节点是红色,就有事另外一种情况了.



if (parent->_col == BLACK)
{
    return true;
}



我们开始处理父亲是红色节点的情况,这里还要分几个情况.其中我们发现后面的两个情况一样,只不过做法不一样



  • 叔叔存在且为红
  • 叔叔不存在或者存在且为黑
  • 叔叔不存在或者存在且为黑



叔叔存存在且为红



我们先来分析这个比较简单的情况,注意我们这个是一个子树,当然有可能是一个完整的树.



AVL树和红黑树的模拟实现_子树_25



具体情况一,abcde都是空树,其中cur是新增的节点,我们父节点是红色,不可能是跟节点点,那么这里一定存在祖父节点间,先暂时假设我下面的是一课完整的树.这里有个问题套讨论.



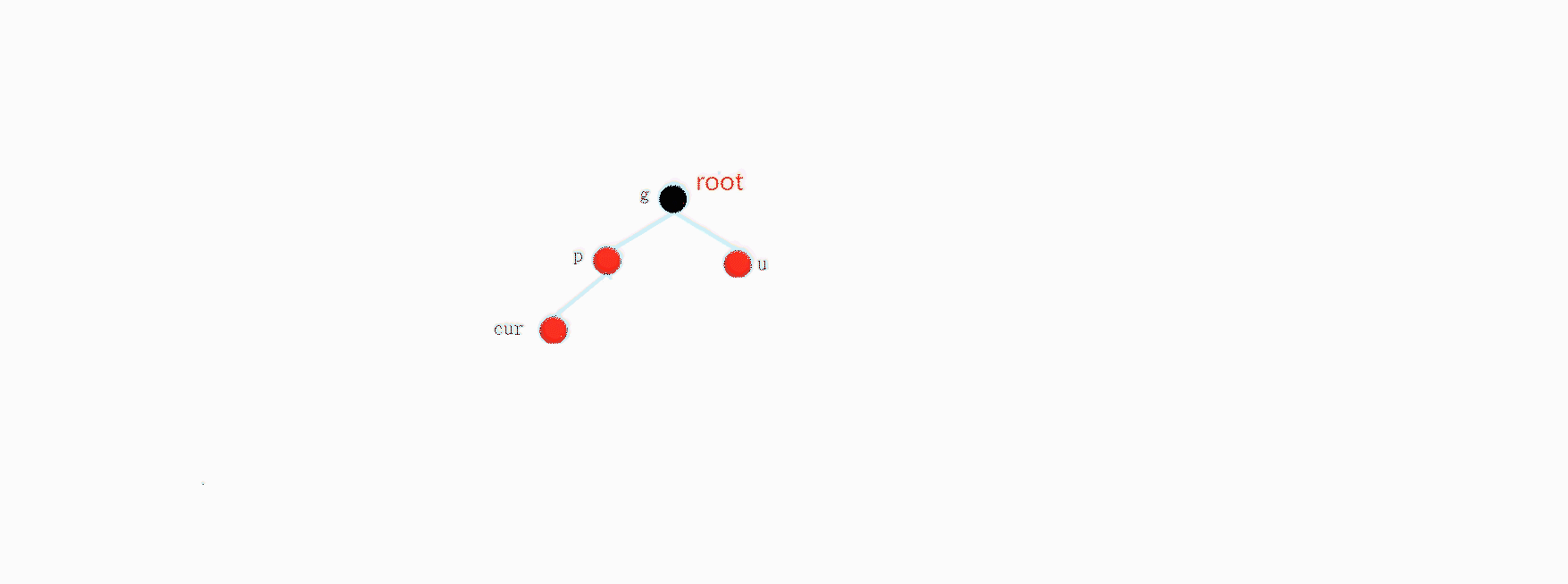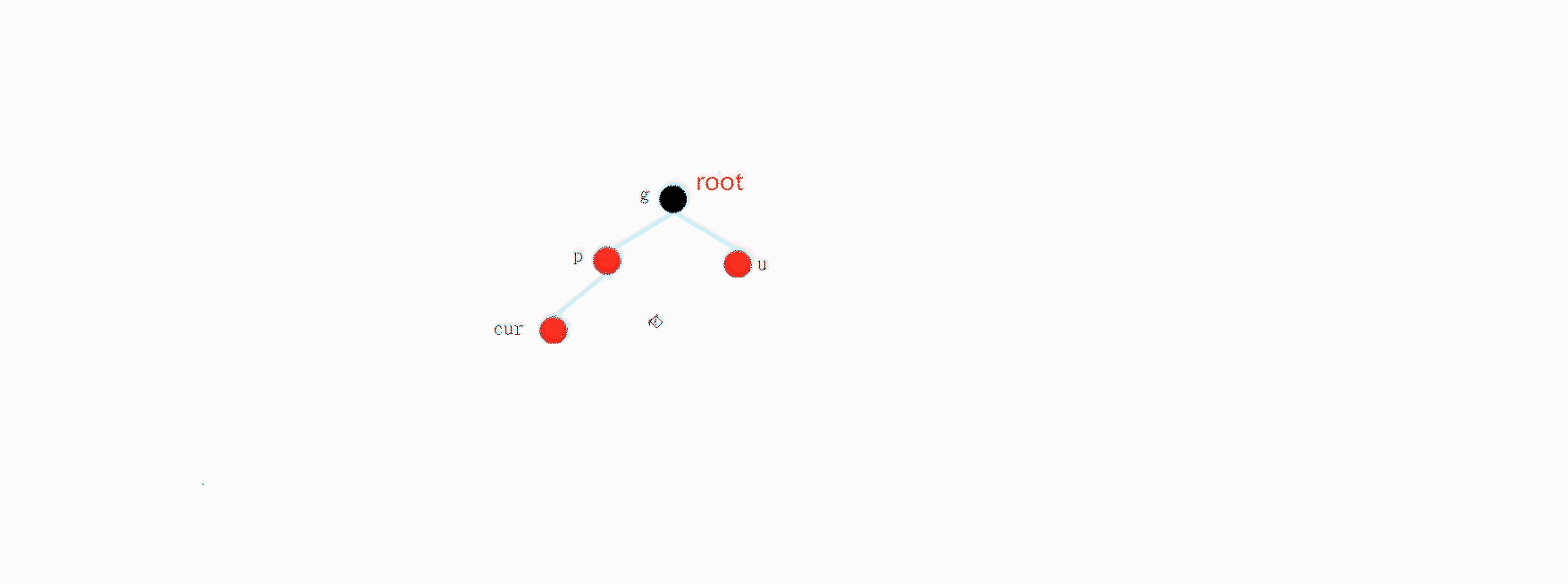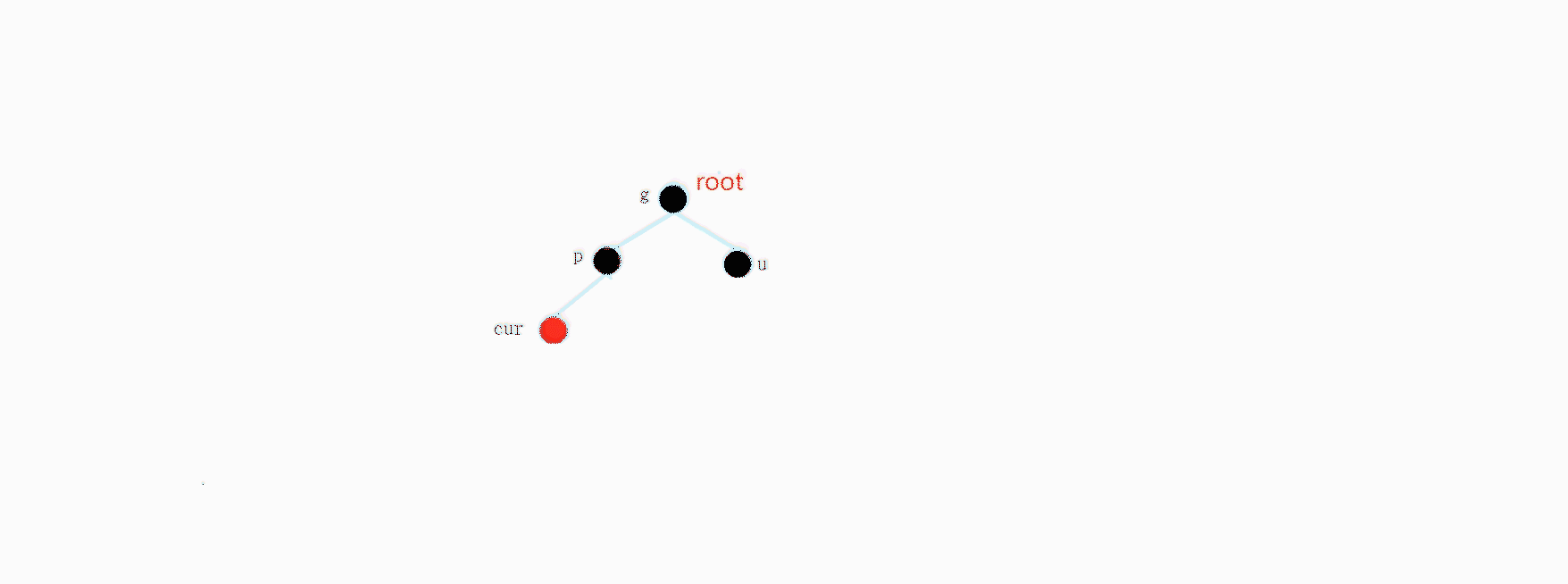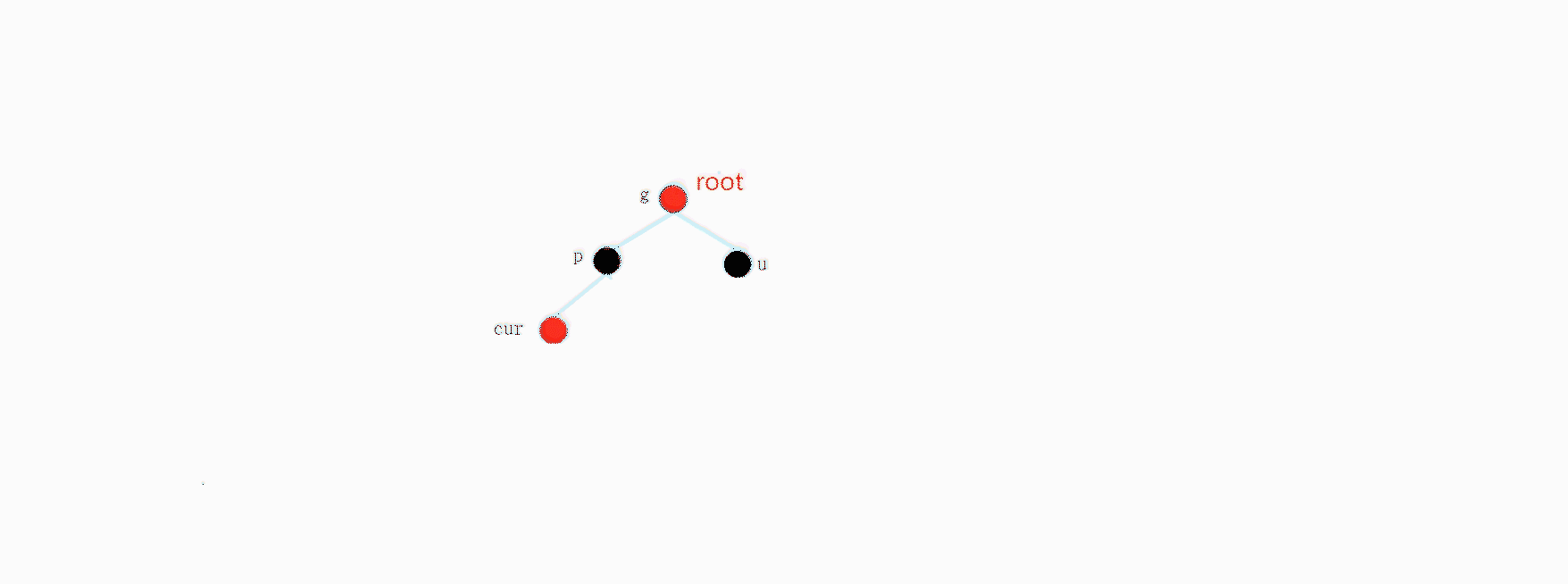
AVL树和红黑树的模拟实现_父节点_26



我们假设是一个完整的树,但是这里根节点变成红色了,不符合要求,等到我们插入完成,最后要修改根节点的颜色,确保他是黑色.



bool Insert(const pair<K, V>& data)
{

//  前期
    //  插入 操作
    _pRoot->_col = BLACK;
    return true;
}



具体情况2,ab不为空树,且是红色.那么cde是下面xyzm中的任意一种,只要存在一个黑色节点就可以了.
那么cur是由黑色变成红色的,也就是我们上面的那一步结束后吧grandfather赋值给cur,再一次进行判断.



由于我们是往上面逐渐改变的,所以后面的情况是很多的,但是不会逃离叔叔存在且为红的限制.这里就不讨论了.



AVL树和红黑树的模拟实现_搜索二叉树_27



具体情况三,判断cur是p的左还是右,p是g的左还是右,这会对情况一造成影响吗?不会的,情况一不关系方向,因为只变色不旋转.我们用情况二举例子



AVL树和红黑树的模拟实现_搜索二叉树_28



while (parent && parent->_col == RED)
{
    Node* grandfather = parent->_parent;
    if (parent->_left == parent)
    {
        // 判断  叔叔节点
        Node* uncle = grandfather->_right;
        if (uncle && uncle->_col == RED)
        {
            // 变色
            parent->_col = BLACK;
            uncle->_col = BALCK;
            grandfather->_col = RED;
            cur = grandfather;
            parent = cur->_parent;
        }
        else  // 叔叔  不存在  或者  存在 是   黑色
        {
        }
    }
    else
    {
        Node* uncle = grandfather->_left;
        //  叔叔 存在  且  为 红
        if (uncle && uncle->_col == RED)
        {
            // 变色
            parent->_col = BLACK;
            uncle->_col = BLACK;
            grandfather->_col = RED;
            cur = grandfather;
            parent = cur->_parent;
        }
        else
        {
        }
    }
}



叔叔不存在或存在且为黑



这个情况是我们红黑树比较难的情况.需要设计到旋转,不过单旋还是比较简单的,这里需要注意的是要如何改变颜色.



AVL树和红黑树的模拟实现_子树_29



叔叔不存在



这个很简单,cur是新增的节点.



AVL树和红黑树的模拟实现_子树_30



具体情况一,abcde都是空树,cur是新增,其中叔叔也是不存在的.你需要把父亲变黑,祖父变红,进行单旋.这里面难得不是旋转,是变色,要保证这棵子树黑色节点不变,那么p变黑,g变红.我们不会让cur变黑的,要是变了为何不直接插入黑色节点.



  • cur是parent的左,parent是grandfather的左,右旋
  • cur是parent的右,parent是grandfather的右,左旋



AVL树和红黑树的模拟实现_父节点_31



存在且为黑



这种情况cur一定不是新增,cur原本是黑色,是由情况一变来的.c 是 xyzm的任意一个,d和e可能空后者为红



AVL树和红黑树的模拟实现_搜索二叉树_32



AVL树和红黑树的模拟实现_搜索二叉树_33



当然上面是我们讨论的最简单的情况,de也可以为黑,只需要加上一层就可以了



AVL树和红黑树的模拟实现_子树_34



这里我就不解释了,反正都要涉及到旋转,只不过是左旋还是右旋的区别.



Node* grandfather = parent->_parent;
if (parent->_left == parent)
{
    // 判断  叔叔节点
    Node* uncle = grandfather->_right;
    if (uncle && uncle->_col == RED)
    {
        // 变色
        parent->_col = BLACK;
        uncle->_col = BALCK;
        grandfather->_col = RED;
        cur = grandfather;
        parent = cur->_parent;
    }
    else  // 叔叔  不存在  或者  存在 是   黑色
    {
        if (cur == parent->_left)
        {
            //     g
            //   p
            // c
            // 右旋
            RotateR(grandfather);
            // 变色
            parent->_col = BLACK;
            grandfather->_col = RED;
        }
        else
        {
        }
        break;
    }
}
else
{
    Node* uncle = grandfather->_left;
    //  叔叔 存在  且  为 红
    if (uncle && uncle->_col == RED)
    {
        // 变色
        parent->_col = BLACK;
        uncle->_col = BLACK;
        grandfather->_col = RED;
        cur = grandfather;
        parent = cur->_parent;
    }
    else
    {
        if (cur == parent->_right)
        {
            //     g
            //       p
            //         c
            // 左旋
            RotateL(grandfather);
            // 变色
            parent->_col = BLACK;
            grandfather->_col = RED;
        }
        else
        {
        }
        break;
    }
}



叔叔不存在或者存在且为黑



我们需要在分析一下这个情况,上面我们会发现我们分析的都是一条直线,和AVL树一样,我们还要考虑双旋的问题.这里就直接和大家演示原理,不在具体的看情况了.



AVL树和红黑树的模拟实现_搜索二叉树_35



Node* grandfather = parent->_parent;
if (parent->_left == parent)
{
    // 判断  叔叔节点
    Node* uncle = grandfather->_right;
    if (uncle && uncle->_col == RED)
    {
        //...
    }
    else  // 叔叔  不存在  或者  存在 是   黑色
    {
        if (cur == parent->_left)
        {
        }
        else
        {
            //   g
            // p
            //    c
            // 左旋 +  右旋
            RotateL(parent);
            RotateR(grandfather);
            cur->_col = BLACK;
            grandfather->_col = RED;
        }
        break;
    }
}
else
{
    Node* uncle = grandfather->_left;
    //  叔叔 存在  且  为 红
    if (uncle && uncle->_col == RED)
    {
    }
    else
    {
        if (cur == parent->_right)
        {
        }
        else
        {
            //   g
            //     p
            //   c
            // 右旋 +  左旋
            RotateR(parent);
            RotateL(grandfather);
            cur->_col = BLACK;
            grandfather->_col = RED;
        }
        break;
    }
}



最后我们旋转写一下就可以了,在AVL树种我们已经分析过了,这里就不解释了.



void RotateL(Node* parent)
{
    Node* sub = parent->_right;
    Node* subR = sub->_left;
    parent->_right = subR;
    if (subR)
        subR->_parent = parent;
    Node* prev = parent->_parent;

sub->_left = parent;
    parent->_parent = sub;
    if (prev == nullptr)
    {
        _pRoot = sub;
        _pRoot->_parent = nullptr;
    }
    else
    {
        if (prev->_left == parent)
            prev->_left = sub;
        else
            prev->_right = sub;

sub->_parent = prev;
    }

}
void RotateR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    parent->_left = subLR;
    if (subLR)
        subLR->_parent = parent;
    Node* prev = parent->_parent;

parent->_parent = subL;
    subL->_right = parent;

//pParent 有可能不是 根
    if (prev == nullptr)
    {
        _pRoot = subL;
        _pRoot->_parent = nullptr;
        return;
    }

if (prev->_left == parent)
        prev->_left = subL;
    else
        prev->_right = subL;

subL->_parent = prev;
}



验证红黑树



我们需要验证一下自己写的红黑树是不是正确的,这里我们需要写一个函数来进行判断.



我们先来看一下中序遍历确保我们是一个二叉搜索树.



int main()
{
  bit::RBTree<int, int> rb;
  for (int i = 0; i < 50; i++)
  {
    if (i == 4)
    {
      cout << endl;
    }
    rb.Insert(make_pair(i, i));
  }

rb.inorder();
  return 0;
}



AVL树和红黑树的模拟实现_父节点_36



我们需要测定一下无序的情况.



int main()
{
  int N = 10;
  srand(time(0));

bit::RBTree<int, int> rb;
  for (int i = 0; i < N; i++)
  {
    int ret = rand();
    rb.Insert(make_pair(ret, ret));
  }

rb.inorder();
  //rb.levelOrder();
  return 0;
}



AVL树和红黑树的模拟实现_子树_37



这里我们在想,如果我们可以知道它的最长路径和最短路径,是不是在一定程度上可以判断是红黑树呢?这种方法不太好,但是一定程度上是可以的.



int main()
{
  int N = 1024;

bit::RBTree<int, int> rb;
  for (int i = 0; i < N; i++)
  {
    rb.Insert(make_pair(i, i));
  }
  cout << rb.maxHeight() << endl;
  cout << rb.minHeight() << endl;

return 0;
}



AVL树和红黑树的模拟实现_搜索二叉树_38



我们发现最长的路径也不会超过最短路径的两倍.但是这也不能确定是不是红色节点连续.下面的方法就对了.



public:   
    bool IsValidRBTree()
    {
        Node* pRoot = _pRoot;
        // 空树也是红黑树
        if (nullptr == pRoot)
            return true;
        // 检测根节点是否满足情况
        if (BLACK != pRoot->_col)
        {
            cout << "违反红黑树性质二：根节点必须为黑色" << endl;
            return false;
        }

// 获取任意一条路径中黑色节点的个数
        size_t blackCount = 0;
        Node* pCur = pRoot;
        while (pCur)
        {
            if (BLACK == pCur->_col)
                blackCount++;
            pCur = pCur->_left;
        }
        // 检测是否满足红黑树的性质，k用来记录路径中黑色节点的个数
        size_t k = 0;
        return _IsValidRBTree(pRoot, k, blackCount);
    }
private:
    bool _IsValidRBTree(Node* pRoot, size_t k, const size_t blackCount)
    {
        //走到null之后，判断k和black是否相等
        if (nullptr == pRoot)
        {
            if (k != blackCount)
            {
                cout << "违反性质四：每条路径中黑色节点的个数必须相同" << endl;
                return false;
            }
            return true;
        }
        // 统计黑色节点的个数
        if (BLACK == pRoot->_col)
            k++;
        // 检测当前节点与其双亲是否都为红色 遇到 红色节点 检查 父亲
        Node* pParent = pRoot->_parent;
        if (pParent && RED == pParent->_col && RED == pRoot->_col)
        {
            cout << "违反性质三：没有连在一起的红色节点" << endl;
            return false;
        }
        return _IsValidRBTree(pRoot->_left, k, blackCount) &&
            _IsValidRBTree(pRoot->_right, k, blackCount);
    }

int main()
{
    int N = 1024;

bit::RBTree<int, int> rb;
    for (int i = 0; i < N; i++)
    {
        rb.Insert(make_pair(i, i));
    }
    cout << "是否平衡 " << rb.IsValidRBTree() << endl;
    return 0;
}



AVL树和红黑树的模拟实现_子树_39

        

        

            

                report
            

        

    







        
Recommend

        



                

    
About Joyk

    
 





Aggregate valuable and interesting links.

Joyk means Joy of geeK