

四色定理和Hadwiger猜想
source link: https://zhuanlan.zhihu.com/p/38071000
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
四色定理和Hadwiger猜想
21世纪前,数学界最著名的猜想之一就是四色猜想了。可能很多人都听说过:对任意的(平面上的)地图染色,要求相邻的国家颜色不同,只需要四种颜色就足够了。
 用四种颜色足够染色地图
用四种颜色足够染色地图这个猜想正式提出是在1852年,其实在之前已经广为流传了。很多数学家尝试从各种角度去接近这个猜想,也提出了各种错误的证明。最终在一个多世纪之后,Appel和Haken在计算机的帮助下证明了这个猜想。不过因为证明主要依靠计算机,至今人们也不是特别清楚,为什么四种颜色就足够了。
我们可以把四色猜想,或者说四色定理,从“地图”等价的转换到“图”上。图,不严谨的说就是点和边连成的图形。在图论中有一个定义叫平面图,说的是一种图可以在平面上画出,并且边之间两两不相交。我们把地图上的每个国家看成一个点,两个国家相邻就代表这两个点之间存在一条边。这样,我们就得到了一个平面图,对国家染色也就变成了对图中的点染色,使得相邻的点不同色。四色定理说,对于任意平面图,四种颜色就足够满足上面的条件了。
很多对四色定理的错误证明源于下面的一个错误观察:很多人觉得,如果对图的点染色,需要四种颜色,一定是因为图的某个区域包含了四个两两相邻的点;同理,如果需要五种颜色,也一定是因为图的某个区域包含了五个两两相邻的点。接下来只要证明,大于等于五个点两两相连的图不能在平面上画出,就证完了。
首先,大于等于五个点两两相连的图,确实是不能在平面画出的。(在图论中, 个点两两相邻的图叫做
阶完全图,记做
)在知乎上我见到了关于这个观点的各种长篇论证,实际上一句话就能说清楚:通过欧拉公式,有
个点的平面图至多有
条边,带入
,我们得到至多
条边。然而五阶完全图有
条边,因此不是平面图。
那么一个图如果不包含五阶完全图,一定可以用四种颜色染色吗?我们考虑弱化的情形,但是原理相同:如果一个图不包含三阶完全图,即三角形,一定两种颜色就够了吗?下面是一个很容易的反例。
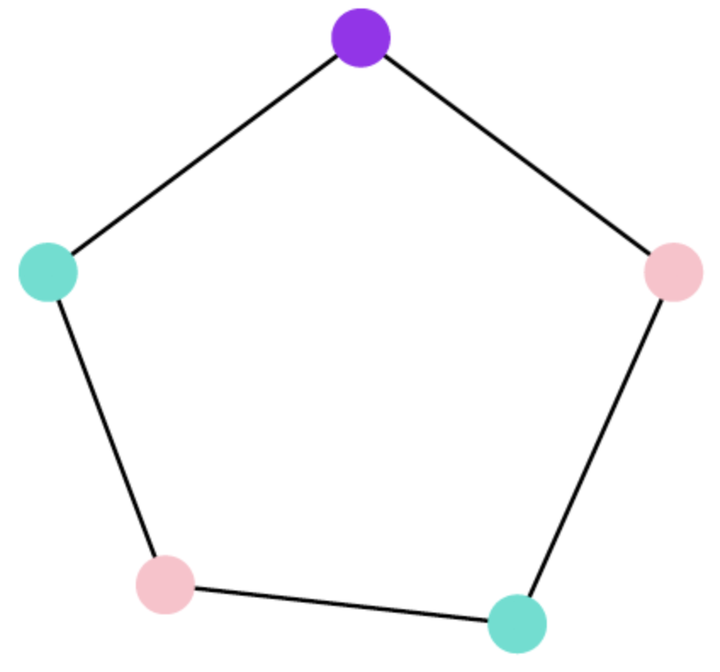 不包含三角形,但是至少需要三种颜色
不包含三角形,但是至少需要三种颜色这告诉我们,试图从图中包含的完全子图的大小来讨论,是错误的方向。实际上Erdos构造了不包含三角形(当然也不包含其他大于三阶的完全图),但是需要染色数任意大的图。
那么,到底是什么力量,在驱使着一个图,需要很多个颜色来染色呢?
这个看起来很自然的问题,人们还不知道。因此图的染色数问题,一直是数学界研究的重点之一。但是人们对此有一些看起来很正确,只等待证明的猜想:比如Hadwiger猜想。这个猜想也是组合数学最深刻的猜想之一,应该也是最没有希望短期内被证明的猜想之一了。在介绍这个猜想之前,我先简单介绍一下Robertson和Seymour引入的一个重要概念:Graph Minor。
其实很类似于矩阵的Minor。一个小的图 是一个大一些的图
的Minor,当且仅当我们可以通过删除
的一些边和点,收缩图
的一些边来得到
,如图。
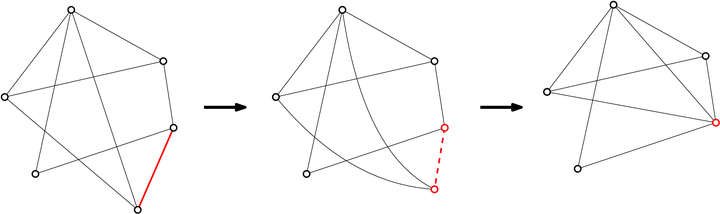 一条边的收缩
一条边的收缩现在,graph minor本身已经成为图论的一个研究重点了,数学家们也相信graph minor是一个正确的研究对象。原因主要是由于Kuratowski定理。Kuratowski定理给了我们平面图的结构,一个图 是平面图当且仅当图
的任何子图不和
与
同胚。Wagner将这个定理稍稍推广了一下,也就是Kuratowski定理的常见形式:
Kuratowski's Theorem
图是平面图当且仅当其不包含
和
做为Minor
Robertson和Seymour成功的将其推广到了任意图:图 可以嵌入亏格为
的曲面,当且仅当其不包含
中的图做为Minor,其中
是一个只由
确定的有限图集。这个定理的成功证明,让数学家相信graph minor是描述图结构的正确语言。
最后回到图的染色问题。刚才我们提到,很多人错误的认为,一个图不包含 阶完全图做为子图,就可以至多用
种颜色染色。我们也给出了一个五边形的反例,五边形不包含
阶完全图,却不能
染色。但是也许我们和事实真相并不远了:
Hadwiger's Conjecture
如果图不包含
阶完全图做为Minor,那么图
至多需要
种颜色染色。
只要把“子图”换成“minor”,一个错误的观察就变成了深刻的猜想。由于人们认为graph minor是正确的语言,因此很多人认为Hadwiger猜想是正确的。不过猜想的进展非常缓慢:
显然。
Hadwiger, 1943
即四色定理,1976
Robertson and Seymour, 1993
数学家对大于等于六的情形一无所知..
如果Hadwiger猜想成立,说明人们已经大致理解任意图的大体结构了。回到最开始提到的五边形的反例:之所以五边形虽然没有三角形,但是需要三种颜色,很可能由于它包含了三角形做为Minor。
五边形包含三角形做为Minor图的染色数一直是一个数学家很想理解又很难理解的东西,四色猜想给了大家一个从图的结构或者拓扑性质入手的契机。数学家想证明黎曼猜想是因为黎曼猜想的推论真的很有用,而数学家想证明四色猜想并不是真的要用四种颜色染地图,而是想搞清楚染色数和图结构的关系。然而Appel和Haken用计算机的证明,并不能告诉我们想要的结果,这也是大家对这个证明有些失望的原因。至今,四色定理没有不依赖计算机的证明。因此图的染色数和结构的关系,伴随Hadwiger猜想,还不是人们目前的智力和技术能探及的区域。
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK